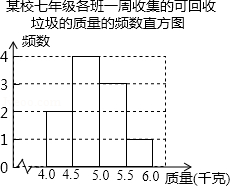
某校积极参与垃圾分类活动,以班级为单位收集可回收垃圾,下面是七年级各班一周收集的可回收垃圾的质量的频数表和频数直方图(每组含前一个边界值,不含后一个边界值).
某校七年级各班一周收集的可回收垃圾的质量的频数表
组别 |
频数 |
|
2 |
|
|
|
3 |
|
1 |
(1)求 的值;
(2)已知收集的可回收垃圾以0.8元 被回收,该年级这周收集的可回收垃圾被回收后所得金额能否达到50元?
相关知识点
推荐套卷


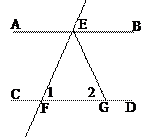
 中,
中, 于
于 ,若
,若 54°,试求
54°,试求 的度数.
的度数. .
.
 粤公网安备 44130202000953号
粤公网安备 44130202000953号