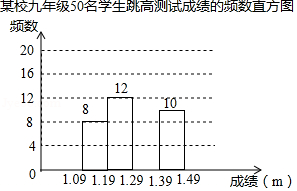
为了了解某校九年级学生的跳高水平，随机抽取该年级50名学生进行跳高测试，并把测试成绩绘制成如图所示的频数表和未完成的频数直方图（每组含前一个边界值，不含后一个边界值）．
某校九年级50名学生跳高测试成绩的频数表
组别 |
频数 |
|
8 |
|
12 |
|
|
|
10 |
（1）求 的值，并把频数直方图补充完整；
（2）该年级共有500名学生，估计该年级学生跳高成绩在 （含 以上的人数．
相关试题
如图，已知在等腰直角三角形
中，
， 
平分
，与
相交于点
，延长
到
，使
，
（1）求证：
；
（2）延长
交
于
，且
，求证：
；
（3）在⑵的条件下，若
是
边的中点，连结
与
相交于点
．
试探索
，
,
之间的数量关系，并证明你的结论．
利用“等积”计算或说理是一种很巧妙的方法， 就是一个面积从两个不同的角度表示。如图甲，已知Rt△ABC中，∠C=90°，CD⊥AB于D，BC=3,AC=4,求CD的长。
解题思路：利用勾股定理易得AB=5利用
，可得到CD=2.4
请你利用上述方法解答下面问题：
（1）如图甲，已知Rt△ABC中，∠C=90°，CD⊥AB于D，BC=5,AC=12,求CD的长。
(2)如图乙，△ABC是边长为2的等边三角形，点D是BC边上的
任意一点，DE⊥AB于E点，DF⊥AC于F点，求DE+DF的值
如图所示：∠ABC的平分线BF与△ABC中∠ACB的相邻外角的平分线CF相交于点F，过F作DF∥BC，交AB于D，交AC于E．
问：（1）图中有几个等腰三角形？为什么？
（2）BD，CE，DE之间存在着什么关系？请证明．
相关知识点
推荐套卷
粤公网安备 44130202000953号