在等腰Rt△ABC中,∠C=90°,AC=1,过点C作直线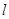 ∥AB,F是
∥AB,F是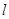 上的一点,且AB=AF,则点F到直线BC的距离为__________
上的一点,且AB=AF,则点F到直线BC的距离为__________
如图是某地下商业街的入口,数学课外兴趣小组的同学打算运用所学的知识测量侧面支架的最高点E到地面的距离EF.经测量,支架的立柱BC与地面垂直,即∠BCA=90°,且BC=1.5m,点F、A、C在同一条水平线上,斜杆AB与水平线AC的夹角∠BAC=30°,支撑杆DE⊥AB于点D,该支架的边BE与AB的夹角∠EBD=60°,又测得AD=1m.请你求出该支架的边BE及顶端E到地面的距离EF的长度.
一次数学活动课上,老师带领学生去测一条南北流向的河宽,如图所示,某学生在河东岸点A处观测到河对岸水边有一点C, 测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈
测得C在A北偏西31°的方向上,沿河岸向北前行40米到达B处,测得C在B北偏西45°的方向上,请你根据以上数据,求这条河的宽度.(参考数值:tan31°≈ )
)
如图,在电线杆CD上的C处引拉线CE、CF固定电线杆,拉线CE和地面所成的角∠CED=60°,在离电线杆6米的B处安置高为1.5米的测角仪AB,在A处测得电线杆上C处的仰角为30°,求拉线CE的长(结果保留小数点后一位,参考数据: ,
, ).
).
如图,在 中, , 是对角线 上的两点(点 在点 左侧),且 .
(1)求证:四边形 是平行四边形;
(2)当 , , 时,求 的长.

如图,将长、宽分别为 , 的长方形纸片分别沿 , 折叠,点 , 恰好重合于点 .若 ,则折叠后的图案(阴影部分)面积为

| A. |
|
B. |
|
C. |
|
D. |
|
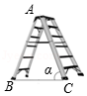
如图是一架人字梯,已知 米, 与地面 的夹角为 ,则两梯脚之间的距离 为
| A. |
米 |
B. |
米 |
C. |
米 |
D. |
米 |
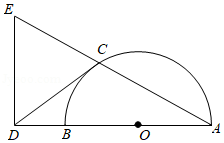
如图,已知点 是以 为直径的半圆上一点, 是 延长线上一点,过点 作 的垂线交 的延长线于点 ,连结 ,且 .
(1)求证: 是 的切线;
(2)若 , ,求 的半径.
数学小组研究如下问题:长春市的纬度约为北纬 ,求北纬 纬线的长度,小组成员查阅了相关资料,得到三条信息:
(1)在地球仪上,与南,北极距离相等的大圆圈,叫赤道,所有与赤道平行的圆圈叫纬线;
(2)如图, 是经过南、北极的圆,地球半径 约为 .弦 ,过点 作 于点 ,连接 .若 ,则以 为半径的圆的周长是北纬 纬线的长度;
(3)参考数据: 取3, , .
小组成员给出了如下解答,请你补充完整:
解:因为 , ,
所以 (填推理依据),
因为 ,所以 ,
在 中, .
(填" "或" " .
所以北纬 的纬线长 .
(填相应的三角形函数值)
(结果取整数).

已知 、 是 的两条弦,直线 、 互相垂直,垂足为 ,连接 ,过点 作 ,垂足为 ,直线 交直线 于点 .
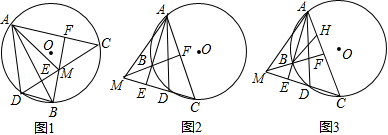
(1)如图1,当点 在 内时,连接 , , ,求证: ;
(2)如图2,当点 在 外时,连接 , ,求证: ;
(3)如图3,当点 在 外时, 的平分线与 交于点 ,若 ,求 的值.
如图所示,在平面直角坐标系 中,等腰 的边 与反比例函数 的图象相交于点 ,其中 ,点 在 轴的正半轴上,点 的坐标为 ,过点 作 轴于点 .
(1)已知一次函数的图象过点 , ,求该一次函数的表达式;
(2)若点 是线段 上的一点,满足 ,过点 作 轴于点 ,连结 ,记 的面积为 ,设 ,
①用 表示 (不需要写出 的取值范围);
②当 取最小值时,求 的值.

如图,已知⊙O的直径AB与弦CD互相垂直,垂足为点E.⊙O的切线BF与弦AC的延长线相交于点F,且AC=8,tan∠BDC= .求线段CF的长.
.求线段CF的长.
如图,某校教学楼AB的后面有一建筑物CD,当光线与地面的夹角是22º时,教学楼在建筑物的墙上留下高2m的影子CE;而当光线与地面的夹角是45º时,教学楼顶A在地面上的影子F与墙角C有13m的距离(B、F、C在一条直线上).求教学楼AB的高度.(参考数据:sin22º≈ ,cos22º≈
,cos22º≈ ,tan22º≈
,tan22º≈ )
)
