初中数学解直角三角形试题

（本题7分）先化简，再求值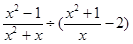：，其中x=2cos30°+tan45.

（1）计算：（-2）^-1-|-|+（-1）⁰+cos45°．
（2））已知m²-5m-14=0，求（m-1）（2m-1）-（m+1）²+1的值．

在△ABC中，若=0，则∠C的度数是（    ）

A．45°

B．60°

C．75°

D．105°

超速行驶是引发交通事故的主要原因之一，小明和三位同学尝试用自己所学的知识检测车速，如图，观测点设在A处，距离大路（BC）为30米，一辆小轿车由西向东匀速行驶，测得此车从B处到C处所用的时间为5秒，∠BAC=60°．

（1）求B、C两点间的距离．
（2）请判断此车是否超过了BC路段限速40千米/小时的速度．（参考数据：≈1．732，≈1．414）

（本题满分12分，每小题6分）
（1）计算
（2）解方程：

下列计算结果正确的是（      ）

A．（-a^3）^2=a^9	B．a^2•a^3=a^6
C．()^−1-2^2=-2	D．(cos60°−)^0=1

在 $\mathit{\Delta ABC}$ 中， $\angle \mathit{ABC}=90°$ ．若 $\mathit{AC}=100$ ， $\sin A=\frac{3}{5}$ ，则 $\mathit{AB}$ 的长是 $($ 　　 $)$

A．

$\frac{500}{3}$

B．

$\frac{503}{5}$

C．

60

D．

80

计算=          ．

计算：+3^﹣2．

在△ABC中，∠C＝90°，sinA＝，则tanB＝_________．

把△ABC三边的长度都扩大为原来的3倍，则锐角A的正弦值函数（   ）

A．不变

B．缩小为原来的

C．扩大为原来的3倍

D．不能确定

如图，在□ABCD中，连接BD，， ， ，则□ABCD的面积是______．

身高相等的四名同学甲、乙、丙、丁参加风筝比赛，四人放出风筝的线长、线与地面的夹角如下表（假设风筝线是拉直的），则四名同学所放的风筝中最高的是（   ）

同学	甲	乙	丙	丁
放出风筝线长	140m	100m	95m	90m
线与地面夹角	30°	45°	45°	60°

 
A．甲              B．乙               C．丙          D．丁

（1）计算：．
（2）先化简，再求值：，其中满足．

按要求解答下列各小题．
（1）计算：；
（2）解方程：.