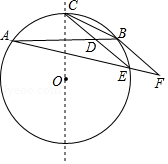
如图所示 为 的一条弦,点 为劣弧 的中点, 为优弧 上一点,点 在 的延长线上,且 ,线段 交弦 于点 .
①求证: ;
②若 ,且 ,求 的面积(注:根据圆的对称性可知 .
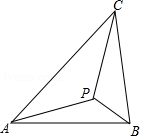
如图示,若 内一点 满足 ,则点 为 的布洛卡点.三角形的布洛卡点 是法国数学家和数学教育家克洛尔 . . 于1816年首次发现,但他的发现并未被当时的人们所注意,1875年,布洛卡点被一个数学爱好者法国军官布洛卡 重新发现,并用他的名字命名.问题:已知在等腰直角三角形 中, ,若点 为 的布洛卡点, ,则
A.5B.4C. D.
如图,将正方形 折叠,使顶点 与 边上的一点 重合 不与端点 , 重合),折痕交 于点 ,交 于点 ,边 折叠后与边 交于点 .设正方形 的周长为 , 的周长为 ,则 的值为

A. B.
C. D.随 点位置的变化而变化
如图,在 中,点 是 边上的一点,若 , , , 的面积为1,则 的面积为

A.1B.2C.3D.4
如图,已知点 、 分别在反比例函数 , 的图象上,且 ,则 的值为
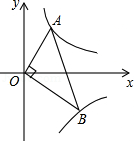
A. B.2C. D.4
如图,四边形 中, , , , ,连接 、 ,以 为直径的圆交 于点 .若 ,则 的长为
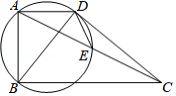
A.5B.4C. D.
如图,直角三角形的直角顶点在坐标原点, ,若点 在反比例函数 的图象上,则经过点 的反比例函数解析式为

A. B. C. D.
如图,在菱形 中, 是 的中点, ,交 于点 ,如果 ,那么菱形 的周长为

A.24B.18C.12D.9
如图,在平行四边形 中, 是 上的点, ,连接 交 于点 ,则 与 的面积之比为

A. B. C. D.
如图,点 是反比例函数 上的一个动点,连接 ,过点 作 ,并且使 ,连接 ,当点 在反比例函数图象上移动时,点 也在某一反比例函数 图象上移动,则 的值为

A. B.4C. D.2
如图, 是 的直径, , 分别与 相交于点 , ,连接 ,现给出两个命题:
①若 ,则 ;
②若 ,记 的面积为 ,四边形 的面积为 ,则 ,
那么

A.①是真命题 ②是假命题B.①是假命题 ②是真命题
C.①是假命题 ②是假命题D.①是真命题 ②是真命题
如图,正方形 中, ,点 在边 上,且 .将 沿 对折至 ,延长 交边 于点 ,连接 、 .下列结论:① ;② ;③ ;④ ;⑤ .其中正确结论的个数是

A.2B.3C.4D.5
如图,在 中,点 在 上, , 交 于 ,则下列结论不正确的是
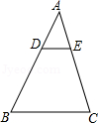
A. B.
C. D.