如图,面积为24的正方形 ABCD中,有一个小正方形 EFGH,其中 E、 F、 G分别在 AB、 BC、 FD上.若 BF= ,则小正方形的周长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
如图,点 P在直线 AB上方,且∠ APB=90°, PC⊥ AB于 C,若线段 AB=6, AC= x, S △ PAB= y,则 y与 x的函数关系图象大致是( )

| A. |
|
B. |
|
| C. |
|
D. |
|
如图,四边形 ABCD是边长为1的正方形, E, F为 BD所在直线上的两点.若 AE= 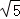 ,∠ EAF=135°,则以下结论正确的是( )
,∠ EAF=135°,则以下结论正确的是( )

| A. |
DE=1 |
B. |
tan∠AFO= |
| C. |
AF= |
D. |
四边形AFCE的面积为 |
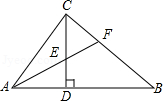
如图,在Rt△ ABC中,∠ ACB=90°, CD⊥ AB,垂足为 D, AF平分∠ CAB,交 CD于点 E,交 CB于点 F.若 AC=3, AB=5,则 CE的长为( )
| A. |
|
B. |
|
C. |
|
D. |
|
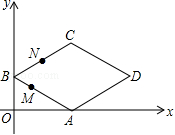
如图,在平面直角坐标系中,四边形 ABCD是菱形,点 B的坐标是(0,4),点 D的坐标 是(8 ,4),点 M和点 N是两个动点,其中点 M从点 B出发,沿 BA以每秒2个单位长度的速度做匀速运动,到点 A后停止,同时点 N从点 B出发,沿折线 BC→ CD以每秒4个单位长度的速度做匀速运动,如果其中一个点停止运动,则另一点也停止运动,设 M, N两点的运动时间为 x,△ BMN的面积为 y,下列图象中能表示 y与 x的函数关系的图象大致是( )
| A. |
|
B. |
|
| C. |
|
D. |
|
如图,在Rt△ ABC中,∠ C=90°, M为 AB边的中点,将Rt△ ABC绕点 M旋转,使点 C与点 A重合得△ DEA, AE交 CB于点 N.若 AB=2 , AC=4,则 CN的长为( )

| A. |
|
B. |
|
C. |
|
D. |
|
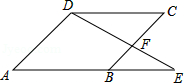
如图, E为▱ ABCD的边 AB延长线上的一点,且 BE: AB=2:3,△ BEF的面积为4,则▱ ABCD的面积为( )
| A. |
30 |
B. |
27 |
C. |
14 |
D. |
32 |
如图, ,
, 分别是双曲线
在第一、三象限上的点,
分别是双曲线
在第一、三象限上的点, 轴,
轴, 轴,垂足分别为
轴,垂足分别为 ,
, ,点
,点 是
是 与
与 轴的交点.设
轴的交点.设 的面积为
的面积为 ,
, 的面积为
的面积为 ,
, 的面积为
的面积为 ,则有
,则有


A. B.
B. C.
C. D.
D.
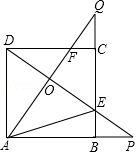
如图,正方形 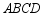 的边长是3,
的边长是3, 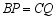 ,连接
,连接 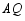 ,
, 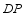 交于点
交于点 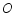 ,并分别与边
,并分别与边 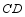 ,
, 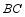 交于点
交于点 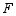 ,
, 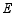 ,连接
,连接  ,下列结论:①
,下列结论:① 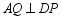 ;②
;② 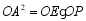 ;③
;③ 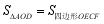 ;④当
;④当 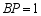 时,
,其中正确结论的个数是
时,
,其中正确结论的个数是 
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
有3个正方形如图所示放置,阴影部分的面积依次记为S1,S2,则S1:S2等于( )

A.1: B.1:2C.2:3D.4:9
B.1:2C.2:3D.4:9
如图,▱ABCD的对角线AC,BD交于点O,CE平分∠BCD交AB于点E,交BD于点F,且∠ABC=60°,AB=2BC,连接OE.下列结论:
①∠ACD=30°;②S▱ABCD=AC•BC;③OE:AC= :6;④S△OCF=2S△OEF
:6;④S△OCF=2S△OEF
成立的个数有( )

A.1个B.2个C.3个D.4个
如图, CB= CA,∠ ACB=90°,点 D在边 BC上(与 B、 C不重合),四边形 ADEF为正方形,过点 F作 FG⊥ CA,交 CA的延长线于点 G,连接 FB,交 DE于点 Q,给出以下结论:
① AC= FG;② S △ FAB: S 四边形 CBFG=1:2;③∠ ABC=∠ ABF;④ AD 2= FQ• AC,
其中正确的结论的个数是( )

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,把某矩形纸片 沿 , 折叠(点 、 在 边上,点 , 在 边上),使点 和点 落在 边上同一点 处, 点的对称点为 、 点的对称点为 ,若 , , ,则矩形 的长为

| A. |
|
B. |
|
C. |
|
D. |
|
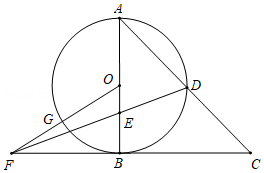
如图,在 中, , ,以 为直径的 交 于点 ,点 为线段 上的一点, ,连接 并延长交 的延长线于点 ,连接 交 于点 ,若 ,则 的长是
| A. |
|
B. |
|
C. |
|
D. |
|