如图1,Rt△ABC两直角边的边长为AC=3,BC=4.
(1)如图2,⊙O与Rt△ABC的边AB相切于点X,与边BC相切于点Y.请你在图2中作出并标明⊙O的圆心(用尺规作图,保留作图痕迹,不写作法和证明)
(2)P是这个Rt△ABC上和其内部的动点,以P为圆心的⊙P与Rt△ABC的两条边相切.设⊙P的面积为S,你认为能否确定S的最大值?若能,请你求出S的最大值;若不能,请你说明不能确定S的最大值的理由.
如图1,已知正方形ABCD的边长为1,点E在边BC上,若∠AEF=900,且EF交正方形外角的平分线CF于点F.
(1)图1中若点E是边BC的中点,我们可以构造两个三角形全等来证明AE=EF,请叙述你的一个构造方案,并指出是哪两个三角形全等(不要求证明);
(2)如图2,若点E在线段BC上滑动(不与点B,C重合).
①AE=EF是否总成立?请给出证明;
②在如图2的直角坐标系中,当点E滑动到某处时,点F恰好落在抛物线 上,求此时点F的坐标.
上,求此时点F的坐标.
四边形 中,
中, ∥
∥ ,
, ,
, ,
, .点
.点 为射线
为射线 上动点(不与点
上动点(不与点 、
、 重合),点
重合),点 在直线
在直线 上,且
上,且 .记
.记 ,
, ,
, ,
, .
.
(1)当点 在线段
在线段 上时,写出并证明
上时,写出并证明 与
与 的数量关系;
的数量关系;
(2)随着点 的运动,(1)中得到的关于
的运动,(1)中得到的关于 与
与 的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的
的数量关系,是否改变?若认为不改变,请证明;若认为会改变,请求出不同于(1)的数量关系,并指出相应的 的取值范围;
的取值范围;
(3)若cos =
= ,试用
,试用 的代数式表示
的代数式表示 .
.
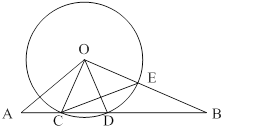
如图,⊙ 的半径为6,线段
的半径为6,线段 与⊙
与⊙ 相交于点
相交于点 、
、 ,
, ,
, ,
, 与⊙
与⊙ 相交于点
相交于点 ,设
,设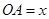 ,
, .
.
(1)求 长;
长;
(2)求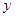 关于
关于 的函数解析式,并写出定义域;
的函数解析式,并写出定义域;
(3)当 ⊥
⊥ 时,求
时,求 的长.
的长.
如图所示,在形状和大小不确定的△ABC中,BC=6,E、F分别是AB.AC的中点,P在EF或EF的延长线上,BP交CE于D,Q在CE上且BQ平分∠CBP,设BP=y,PE=x.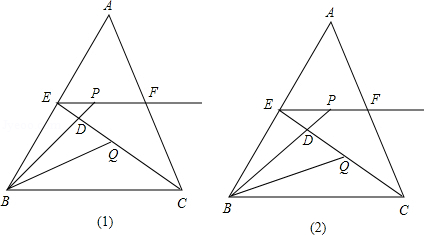
(1)当x= EF时,求S△DPE:S△DBC的值;
EF时,求S△DPE:S△DBC的值;
(2)当CQ= CE时,求y与x之间的函数关系式;
CE时,求y与x之间的函数关系式;
(3)①当CQ= CE时,求y与x之间的函数关系式;
CE时,求y与x之间的函数关系式;
②当CQ= CE(n为不小于2的常数)时,直接写出y与x之间的函数关系式.
CE(n为不小于2的常数)时,直接写出y与x之间的函数关系式.
如图,在平面直角坐标系xOy中,矩形OEFG的顶点E的坐标为(4,0),顶点G的坐标为(0,2),将矩形OEFG绕点O逆时针旋转,使点F落在y轴的点N处,得到矩形OMNP,OM与GF交于点A.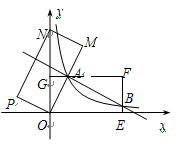
(1)判断△OGA和△OMN是否相似,并说明理由;
(2)求图象经过点A的反比例函数的解析式;
(3)设(2)中的反比例函数图象交EF于点B,求直线AB的解析式.
如图所示, ,
, ,
, ,点
,点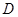 是以
是以 为直径的半圆
为直径的半圆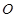 上一动点,
上一动点,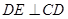 交直线
交直线 于点
于点 ,设
,设 .
.当
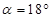 时,求
时,求 的长;
的长;当
 时,求线段
时,求线段 的长;
的长;若要使点
 在线段
在线段 的延长线上,则
的延长线上,则 的取值范围是_______.(直接写出答案)
的取值范围是_______.(直接写出答案)
右图中,ABCD是梯形,面积是1。已知 =
=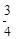 ,
,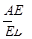 =
= ,
, =
=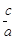 。问:
。问:

(1) 三角形ECD的面积是多少?
(2) 四边形EHFG的面积是多少?
如图,在△ABC中,AB=8,BC=7,AC=6,延长边BC到点P,使得△PAB与△PCA相似.则PC的长是( ). 
| A.7 | B.8 | C.9 | D.10 |
(25分)如图,在Rt△ABC中,∠B=90°,它的内切圆分别与边BC、CA、AB相切于点D、E、F,联结AD与内切圆相交于另一点P,联结PC、PE、PF.已知PC⊥PF.求证:
(1)EP/DE=PD/DC;(2)△EPD是等腰三角形.