如图所示,一段街道的两边缘所在直线分别为AB,PQ,并且AB∥PQ.建筑物的一端DE所在的直线MN⊥AB于点M,交PQ于点N.小亮从胜利街的A处,沿着AB方向前进,小明一直站在点P的位置等候小亮.
(1)请你在图中画出小亮恰好能看见小明时的视线,以及此时小亮所在位置(用点C标出);
(2)已知:MN=20m,MD=8m,PN=24m,求(1)中的点C到胜利街口的距离CM.
如图,某居民小区有一朝向为正南方向的居民楼,该居民楼的一楼是高6米的小区超市,超市以上是居民住房,在该楼的前面16米处要盖一栋高20米的新楼,在冬至日清晨阳光的照射下,1米高的小树的影子长为1.6米.
(1)问超市以上的居民住房采光是否受到影响?为什么?
(2)若要使超市以上的居民住房采光不受影响,两楼应相距多少米?
已知在△ABC中,∠ABC=90°,AB=3,BC=4.点Q是线段AC上的一个动点,过点Q作AC的垂线交线段AB(如图1)或线段AB的延长线(如图2)于点P.
(1)当点P在线段AB上时,求证:△AQP∽△ABC;
(2)当△PQB为等腰三角形时,求AP的长.
如图,在△ABC中,∠ABC=2∠C,BD平分∠ABC,且 ,
, ,求AB的值.
,求AB的值.
如图△ABC中,DE∥BC,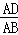 =
=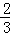 ,M为BC上一点,AM交DE于N.
,M为BC上一点,AM交DE于N.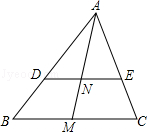
(1)若AE=4,求EC的长;
(2)若M为BC的中点,S△ABC=36,求S△ADN.
已知:△ABC在直角坐标平面内,三个顶点的坐标分别为A(0,3)、B(3,4)、C(2,2)(正方形网格中每个小正方形的边长是一个单位长度).

(1)画出△ABC向下平移4个单位长度得到的△A1B1C1,点C1的坐标是 ;
(2)以点B为位似中心,在网格内画出△A2B2C2,使△A2B2C2与△ABC位似,且位似比为2:1,点C2的坐标是 ;
(3)△A2B2C2的面积是 平方单位.
如图,平行四边形ABCD中,AE:EB=1:2,求△AEF与△CDF的周长的比.如果S△AEF=6cm2,
求S△CDF.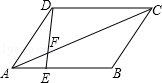
如图,在Rt△ABC中,∠ACB=90°,AC=6,BC=8,点D以每秒1个单位长度的速度由点A向点B匀速运动,到达B点即停止运动,M,N分别是AD,CD的中点,连接MN,设点D运动的时间为t.
(1)判断MN与AC的位置关系;
(2)求点D由点A向点B匀速运动的过程中,线段MN所扫过区域的面积;
(3)若△DMN是等腰三角形,求t的值.
如图,在平行四边形ABCD中,过点A作AE⊥BC,垂足为E,连接DE,F为线段DE上一点,且∠AFE=∠B.
(1)求证:△ADF∽△DEC
(2)若AB=4,AD=3 ,AE=3,求AF的长.
,AE=3,求AF的长.
如图,在边上为1个单位长度的小正方形网格中:
(1)画出△ABC向上平移6个单位长度,再向右平移 5个单位长度后的△A1B1C1.
(2)以点B为位似中心,将△ABC放大为原来的2倍,得到△A2B2C2,请在网格中画出△A2B2C2.
(3)求△CC1C2的面积.
如图,在平面直角坐标系中,直线AB与x轴,y轴分别交于点A(4,0),B(0,3).点C的坐标为(0,m),过点C作CE⊥AB于点E,点D为x轴正半轴的一动点,且满足OD=2OC,连结DE,以DE,DA为边作□DEFA.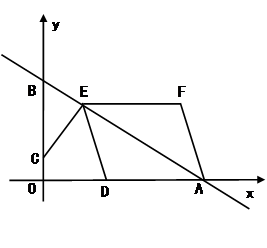
(1)当m=1时,求AE的长.
(2)当0<m<3时,若□DEFA为矩形,求m的值;
(3)是否存在m的值,使得□DEFA为菱形?若存在,直接写出m的值;若不存在,请说明理由.
幼儿园购买了一个板长AB=4m,支架OC高0.8m的翘翘板,支点O在板AB的中点.因支架过高不宜小朋友玩,故把它暂时存放在高2.4m的车库里,准备改装.现有几个小朋友把板的一端A按到地面上.
(1)板的另一端B会不会碰到车库的顶部;
(2)能否通过移动支架,使B点恰好碰到车库的顶部?若能,求出此时支点O的位置;若不能,请说明理由.
如图,⊙O中,弦AB、CD相交于AB的中点E,连接AD并延长至点F,使DF=AD,连接BC、BF.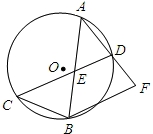
(1)求证:△CBE∽△AFB;
(2)当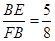 时,求
时,求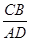 的值.
的值.
如图,现有一个边长是1的正方形ABCD,在它的左侧补一个矩形ABEF,使所得矩形CEFD相似于矩形ABEF,求BE的长.
如图,在△ABC中,D,E,F分别是边AB,AC,BC上的点,且DE∥BC,EF∥AB,AD:DB=3:2,BC=20㎝,求FC的长.