如图1,在正方形ABCD中,延长BC至M,使BM=DN,连接MN交BD延长线于点E.
(1)求证:BD+2DE= BM.
BM.
(2)如图2,连接BN交AD于点F,连接MF交BD于点G.若AF:FD=1:2,且CM=2,则线段DG= .

如图,△ABC中,∠C=90°,AC=3cm,BC=4cm,动点P从点B出发以2cm/s的速度向点C移动,动点Q从C出发以1cm/s的速度向点A移动,如果动点P、Q同时出发,要使△CPQ与△CBA相似,所需要的时间是多少秒?
如图,若∠DAB=∠CAE,∠B=∠D,AD=4,DE=5,AB=6,求BC的长.
如图,Rt△ABC中,∠C=90°,AC=6cm,BC=8cm,一动点P从点A出发沿边AC向点C以1cm/s的速度运动,另一动点Q同时从点C出发沿CB边向点B以2cm/s的速度运动.问: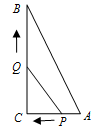
(1)运动几秒时,△CPQ的面积是8cm2?
(2)运动几秒时,△CPQ与△ABC相似?
已知:点A(-3,0),点B(1,3),点C(1,0).
(1)请在x轴上找一点D,使得△BDA与△BAC相似(不包含全等),并求出点D的坐标;
(2)在(1)的条件下,如果P、Q分别是AB、AD上的动点,连结PQ,设AP=DQ=m,问:是否存在这样的m,使得△APQ与△BDA相似?如存在,请求出m的值;若不存在,请说明理由.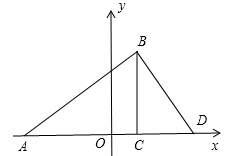
我们在学习三角形相似时,往往是添加平行线构造相似三角形的基本图形.有一学生根据这一理论猜想三角形内角平分线有这样一个性质:如图,在△ABC中,AD平分∠BAC,则 .如果你认为这个猜想是正确的,请写出一个完整的推理过程.
.如果你认为这个猜想是正确的,请写出一个完整的推理过程.
如图,在由边长为1的单位正方形组成的网格中,按要求画出坐标系及△A1B1C1及△A2B2C2;
(1)若点A、C的坐标分别为(-3,0)、(-2,3),请画出平面直角坐标系并指出点B的坐标;
(2)画出△ABC关于 轴对称再向上平移1个单位后的图形△A1B1C1;
轴对称再向上平移1个单位后的图形△A1B1C1;
(3)在网格范围内,以图中的点D为位似中心,将△A1B1C1作位似变换且把边长放大到原来的两倍,得到△A2B2C2.
如图,在正方形ABCD中,E为BC上任意一点(与B、C不重合),∠AEF=90°.观察图形:
(1)△ABE 与△ECF 是否相似?并证明你的结论.
(2)若E为BC的中点,连结AF,图中有哪些相似三角形?并说明理由.
△ABC为锐角三角形,AD是边BC上的高,正方形EFGH的一边EF在BC上,顶点G,H分别在AC,AB上,BC=30,AD=20.求这个正方形的边长.
如图,四边形ABCD中,AC平分∠DAB,∠ADC=∠ACB=90°,E为AB的中点,
(1)求证:AC2=AB•AD;
(2)求证:CE∥AD;
(3)若AD=4,AB=6,求 的值.
的值.