如图，在正方形ABCD中，E为BC上任意一点（与B、C不重合），∠AEF=90°．观察图形：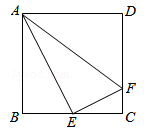
（1）△ABE 与△ECF 是否相似？并证明你的结论．
（2）若E为BC的中点，连结AF，图中有哪些相似三角形？并说明理由．
，且
异号，
是绝对值最小的负整数，
，求3A·B-
A·C的值.
，其中
.
；相关知识点
推荐套卷
如图，在正方形ABCD中，E为BC上任意一点（与B、C不重合），∠AEF=90°．观察图形：
（1）△ABE 与△ECF 是否相似？并证明你的结论．
（2）若E为BC的中点，连结AF，图中有哪些相似三角形？并说明理由．
粤公网安备 44130202000953号