初中数学相似多边形的性质解答题

如图，已知AC，EC分别为正方形ABCD和正方形EFCG的对角线，点E在△ABC内，连接BF，∠CAE+∠CBE=90°．

（1）求证：△CAE∽△CBF；
（2）若BE=1，AE=2，求CE的长．

如图，△ABC中，CD是边AB上的高，且．

（1）求证：△ACD∽△CBD；
（2）求∠ACB的大小．

如图，小明同学用自制的直角三角形纸板DEF测量树的高度AB，他调整自己的位置，设法使斜边DF保持水平，并且边DE与点B在同一直线上，已知纸板的两条直角边DE=40cm，EF=20cm，测得边DF离地面的高度AC=1．5m，CD=8m，求树高AB．

如图，DE∥BC，EF∥CG，AD：AB=1：3，AE=3．

（1）求EC的值；
（2）求证：AD•AG=AF•AB．

阅读理解：如图①，在四边形ABCD的边AB上任取一点E（点E不与A、B重合），分别连接ED、EC，可以把四边形ABCD分成三个三角形，如果其中有两个三角形相似，我们就把E叫做四边形ABCD的边AB上的“相似点”；如果这三个三角形都相似，我们就把E叫做四边形ABCD的边AB上的“强相似点”．解决问题：
（1）如图①，∠A=∠B=∠DEC=45°，试判断点E是否是四边形ABCD的边AB上的相似点，并说明理由；
（2）如图②，在矩形ABCD中，A、B、C、D四点均在正方形网格（网格中每个小正方形的边长为1）的格点（即每个小正方形的顶点）上，试在图②中画出矩形ABCD的边AB上的强相似点；
（3）如图③，将矩形ABCD沿CM折叠，使点D落在AB边上的点E处，若点E恰好是四边形ABCM的边AB上的一个强相似点，试探究AB与BC的数量关系．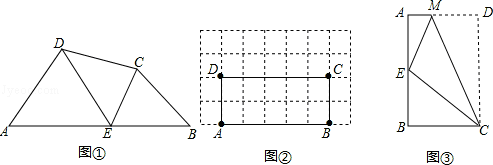

如图，在正方形ABCD中，E为边AD的中点，且DF：CF=1：3，连接EF并延长交BC的延长线于点G，

（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长．

如图，矩形ABCD中，AB=6，BC=10，点P在边BC上，点Q在边CD上，

（1）如图1，将△ADQ沿AQ折叠，点D恰好与点P重合，求CQ的长；
（2）如图2，若CQ=2，且△ABP与△PCQ相似，求BP的长；
（3）若点Q是CD边上的一点，且BC上不存在满足AP⊥PQ的点P，请探究：此时CQ的长必须满足什么条件？

己知：如图，在菱形ABCD中，点M、N分别在边AD、AB，∠DCM=∠BCN，CN与BD交于点E．

（1）求证：DM=BN；
（2）当四边形MNBE是平行四边形时，求证：．

在平面直角坐标系中，△ABC的三个顶点坐标分别为A（2，﹣4），B（3，﹣2），C（6，﹣3）．

（1）画出△ABC关于x轴对称的△A₁B₁C₁；
（2）以M点为位似中心，在网格中画出△A₁B₁C₁的位似图形△A₂B₂C₂，使△A₂B₂C₂与△A₁B₁C₁的相似比为2∶1．
（3）请写出（2）中放大后的△A₂B₂C₂中A₂B₂边的中点P的坐标．．

如图，在Rt△ABC中，∠C=90°，AC=4cm，BC=3cm．动点M，N从点C同时出发，均以每秒1cm的速度分别沿CA、CB向终点A，B移动，同时动点P从点B出发，以每秒2cm的速度沿BA向终点A移动，连接PM，PN，设移动时间为t（单位：秒，0＜t＜2．5）．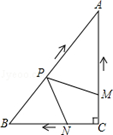

（1）当t为何值时，以A，P，M为顶点的三角形与△ABC相似？
（2）是否存在某一时刻t，使四边形APNC的面积S有最小值？若存在，求S的最小值；若不存在，请说明理由．

如图，在边长为1个单位长度的小正方形组成的网格中，按要求画出△A₁B₁C₁和△A₂B₂C₂；                  

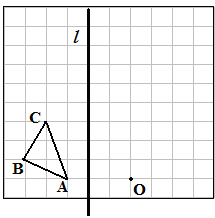
（1）先作△ABC关于直线成轴对称的图形，再向上平移1个单位，得到△A₁B₁C₁；
（2）以图中的O为位似中心，将△A₁B₁C₁作位似变换且放大到原来的两倍，得到△ A₂B₂C₂．

如图所示的一张矩形纸片（），将纸片折叠一次，使点与重合，再展开，折痕交边于，交边于，AC与EF交于点O,分别连结和．在线段上是否存在一点，使得2AE²=AC·AP？若存在，请说明点的位置，并予以证明；若不存在，请说明理由．

如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB的中点，


（1）求证：AC²＝AB•AD；
（2）求证：CE∥AD；
（3）若AD＝4，AB＝6，求的值．

如图，四边形ABCD中，AC平分∠DAB，∠ADC＝∠ACB＝90°，E为AB中点．

（1）求证：AC²＝AB•AD；
（2）若AD＝4，AB＝6，求的值．

已知，△ABC在直角坐标平面内，三个顶点的坐标分别为A（－2， 2）、B（－1，0）、C（0，1）（正方形网格中每个小正方形的边长是一个单位长度）．

（1）画出△ABC关于y轴的轴对称图形△A₁B₁C₁；
（2）以点O为位似中心，在网格内画出所有符合条件的△A₂B₂C₂，使△A₂B₂C₂与△A₁B₁C₁位似，且位似比为2：1；
（3）求△A₁B₁C₁与△A₂B₂C₂的面积比．