已知点A、B分别在反比例函数 (x>0),
(x>0), (x>0)的图象上,且OA⊥OB,则
(x>0)的图象上,且OA⊥OB,则 的值为( )
的值为( )
A. B.2 C.
B.2 C.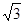 D.3
D.3
如图,点E、F分别为正方形ABCD中AB、BC边的中点,连接AF、DE相交于点G,连接CG,则cos∠CGD=( )
A. B.
B. C.
C. D.
D.

如图,AD为等边△ABC边BC上的高,AB=4,AE=1,P为高AD上任意一点,则EP+BP的最小值为( )。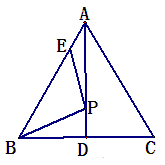
A.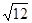 |
B.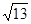 |
C.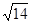 |
D.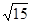 |
如图(1),E为矩形ABCD边AD上一点,点P从点B沿折线BE-ED-DC运动到点C时停止,点Q从点B沿BC运动到点C时停止,它们运动的速度都是1cm/s.如果点P、Q同时开始运动,设运动时间为t(s),△BPQ的面积为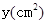 ,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )
,已知y与t的函数关系的图象如图(2)所示,那么下列结论正确的是( )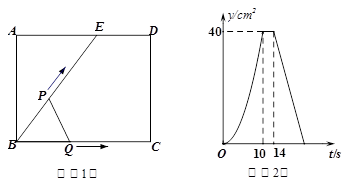
| A.AE=8 |
B.当0≤t≤10时,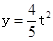 |
C.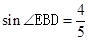 |
D.当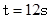 时,△BPQ是等腰三角形 时,△BPQ是等腰三角形 |
如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是
A. B.
B. C.
C. D.
D.
如图,在△ABC中,AB=AC=a,BC=b(a>b).在△ABC内依次作∠CBD=∠A,∠DCE=∠CBD,∠EDF=∠DCE.则EF等于
A. |
B. |
C. |
D. |
在平面坐标系中,正方形ABCD的位置如图所示,点A的坐标为(1,0),点D的坐标为(0,2),延长CB交x轴于点A1,作正方形A1B1C1C,延长C1B1交x轴于点A2,作正方形A2B2C2C1,…按这样的规律进行下去,第2012个正方形的面积为( )
A.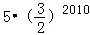 |
B.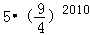 |
C.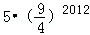 |
D.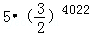 |
如图,矩形ABCD中,E是BC的中点,连接AE,过点E作EF⊥AE交DC于点F,连接AF.设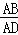 =k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )
=k,下列结论:(1)△ABE∽△ECF,(2)AE平分∠BAF,(3)当k=1时,△ABE∽△ADF,其中结论正确的是( )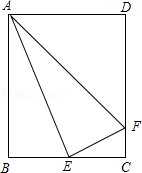
| A.(1)(2)(3) | B.(1)(3) | C.(1)(2) | D.(2)(3) |
如图,直线y=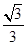 x+
x+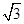 与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )
与x轴、y轴分别相交于A、B两点,圆心P的坐标为(1,0),⊙P与y轴相切于点O.若将⊙P沿x轴向左移动,当⊙P与该直线相交时,满足横坐标为整数的点P的个数是( )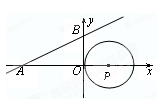
A.3 B.4 C.5 D.6
图(1)中的梯形符合_______条件时,可以经过旋转和翻折形成图案(2).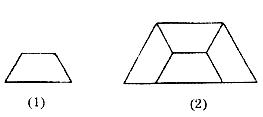
如图, 是
是 的直径,
的直径, 是
是 的切线,点
的切线,点 在
在 上,
上, ,
, 则
则 的长为( )
的长为( )
A. |
B. |
C. |
D. |

如图,△ABC≌△ADE且∠ABC=∠ADE,∠ACB=∠AED,BC.DE交于点O.则下列四个结论中,①∠1=∠2;②BC=DE;③△ABD∽△ACE;④A.O、C.E四点在同一个圆上,一定成立的有( )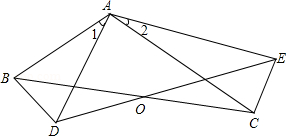
A. 1个 B. 2个 C. 3个 D. 4个
如图,在Rt△ABC内有边长分别为a,b,c的三个正方形,则a,b,c满足的关系式为
| A.b=a+c | B.b=ac | C.b2=a2+c2 | D.b=2a=2c |
如图,梯子共有7级互相平行的踏板,每相邻两级踏板之间的距离都相等.已知梯子最上面一级踏板的长度A1B1 = 0.5m,最下面一级踏板的长度A7B7 = 0.8m.则第五级踏板A5B5的长度为 ( )
| A.0.6m | B.0.65m | C.0.7m | D.0.75m |
观察右图,在下列四种图形变换中,该图案不包含的变换是【 】
| A.平移 | B.轴对称 | C.旋转 | D.位似 |