[辽宁]2013年初中毕业升学考试(辽宁铁岭卷)数学
在一个不透明的口袋中装有4个红球和若干个白球,他们除颜色外其他完全相同.通过多次摸球实验后发现,摸到红球的频率稳定在25%附近,则口袋中白球可能有
| A.6个 | B.15个 | C.13个 | D.12个 |
如图是4块小立方块所搭成的几何体的俯视图,小正方形中的数字表示该位置小方块的个数,其主视图是
A. |
B. |
C. |
D. |
如图,在△ABC和△DEB中,已知AB=DE,还需添加两个条件才能使△ABC≌△DEC,不能添加的一组条件是
| A.BC=EC,∠B=∠E | B.BC=EC,AC=DC |
| C.BC=DC,∠A=∠D | D.∠B=∠E,∠A=∠D |
某工厂生产一种零件,计划在20天内完成,若每天多生产4个,则15天完成且还多生产10个.设原计划每天生产x个,根据题意可列分式方程为
A. |
B.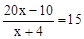 |
C.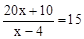 |
D.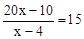 |
如果三角形的两边长分别是方程x2﹣8x+15=0的两个根,那么连接这个三角形三边的中点,得到的三角形的周长可能是
| A.5.5 | B.5 | C.4.5 | D.4 |
如图,点G、E、A、B在一条直线上,Rt△EFG从如图所示是位置出发,沿直线AB向右匀速运动,当点G与B重合时停止运动.设△EFG与矩形ABCD重合部分的面积为S,运动时间为t,则S与t的图象大致是
A. B.
B. C.
C. D.
D.
某商店压了一批商品,为尽快售出,该商店采取如下销售方案:将原来每件m元,加价50%,再做两次降价处理,第一次降价30%,第二次降价10%.经过两次降价后的价格为 元(结果用含m的代数式表示)
如图,点P是正比例函数y=x与反比例函数 在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是 .
在第一象限内的交点,PA⊥OP交x轴于点A,△POA的面积为2,则k的值是 .
如图,在△ABC中,AB=2,BC=3.6,∠B=60°,将△ABC绕点A按顺时针旋转一定角度得到△ADE,当点B的对应点D恰好落在BC边上时,则CD的长为 .
如图,在平面直角坐标中,直线l经过原点,且与y轴正半轴所夹的锐角为60°,过点A(0,1)作y轴的垂线l于点B,过点B1作作直线l的垂线交y轴于点A1,以A1B.BA为邻边作 ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作
ABA1C1;过点A1作y轴的垂线交直线l于点B1,过点B1作直线l的垂线交y轴于点A2,以A2B1.B1A1为邻边作 A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
A1B1A2C2;…;按此作法继续下去,则Cn的坐标是 .
如图,△ABC中,AB=AC,AD是△ABC的角平分线,点O为AB的中点,连接DO并延长到点E,使OE=OD,连接AE,BE.
(1)求证:四边形AEBD是矩形;
(2)当△ABC满足什么条件时,矩形AEBD是正方形,并说明理由.
为迎接十二运,某校开设了A:篮球,B:毽球,C:跳绳,D:健美操四种体育活动,为了解学生对这四种体育活动的喜欢情况,在全校范围内随机抽取若干名学生,进行问卷调查(每个被调查的同学必须选择而且只能在4中体育活动中选择一种).将数据进行整理并绘制成以下两幅统计图(未画完整).
(1)这次调查中,一共查了 名学生:
(2)请补全两幅统计图:
(3)若有3名最喜欢毽球运动的学生,1名最喜欢跳绳运动的学生组队外出参加一次联谊互活动,欲从中选出2人担任组长(不分正副),求两人均是最喜欢毽球运动的学生的概率.
如图,△ABC内接与⊙O,AB是直径,⊙O的切线PC交BA的延长线于点P,OF∥BC交AC于AC点E,交PC于点F,连接AF.
(1)判断AF与⊙O的位置关系并说明理由;
(2)若⊙O的半径为4,AF=3,求AC的长.
如图所示,某工程队准备在山坡(山坡视为直线l)上修一条路,需要测量山坡的坡度,即tanα的值.测量员在山坡P处(不计此人身高)观察对面山顶上的一座铁塔,测得塔尖C的仰角为37°,塔底B的仰角为26.6°.已知塔高BC=80米,塔所在的山高OB=220米,OA=200米,图中的点O、B、C、A、P在同一平面内,求山坡的坡度.(参考数据sin26.6°≈0.45,tan26.6°≈0.50;sin37°≈0.60,tan37°≈0.75)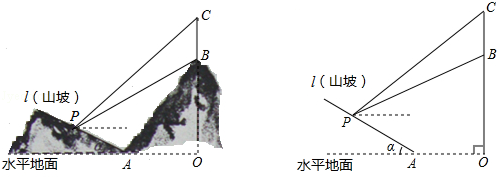
某商家独家销售具有地方特色的某种商品,每件进价为40元.经过市场调查,一周的销售量y件与销售单价x(x≥50)元/件的关系如下表:
| 销售单价x(元/件) |
… |
55 |
60 |
70 |
75 |
… |
| 一周的销售量y(件) |
… |
450 |
400 |
300 |
250 |
… |
(1)直接写出y与x的函数关系式: .
(2)设一周的销售利润为S元,请求出S与x的函数关系式,并确定当销售单价在什么范围内变化时,一周的销售利润随着销售单价的增大而增大?
(3)雅安地震牵动亿万人民的心,商家决定将商品一周的销售利润全部寄往灾区,在商家购进该商品的贷款不超过10000元情况下,请你求出该商家最大捐款数额是多少元?
正方形ABCD中,点E、F分别是边AD、AB的中点,连接EF.
(1)如图1,若点G是边BC的中点,连接FG,则EF与FG关系为: ;
(2)如图2,若点P为BC延长线上一动点,连接FP,将线段FP以点F为旋转中心,逆时针旋转900,得到线段FQ,连接EQ,请猜想EF、EQ、BP三者之间的数量关系,并证明你的结论;
(3)若点P为CB延长线上一动点,按照(2)中的作法,在图3中补全图形,并直接写出EF、EQ、BP三者之间的数量关系: .
如图,抛物线 的对称轴是直线x=
的对称轴是直线x=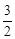 ,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).
,与x轴交于点A、B两点,与y轴交于点C,并且点A的坐标为(—1,0).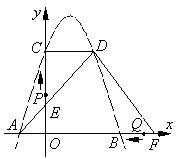
(1)求抛物线的解析式;
(2)过点C作CD//x轴交抛物线于点D,连接AD交y轴于点E,连接AC,设△AEC的面积为S1, △DEC的面积为S2,求S1:S2的值;
(3)点F坐标为(6,0),连接D,在(2)的条件下,点P从点E出发,以每秒3个单位长的速度沿E→C→D→F匀速运动;点Q从点F出发,以每秒2个单位长的速度沿F→A匀速运动,当其中一点到达终点时,另外一点也随之停止运动.若点P、Q同时出发,设运动时间为t秒,当t为何值时,以D、P、Q为顶点的三角形是直角三角形?请直接写出所有符合条件的t值..
 的绝对值是
的绝对值是










 的解集,其中正确的是
的解集,其中正确的是



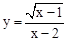 有意义,则自变量x的取值范围是 .
有意义,则自变量x的取值范围是 . ,则成绩比较稳定的是 (填“甲”或“乙”)
,则成绩比较稳定的是 (填“甲”或“乙”)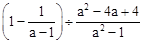 ,其中a=﹣2.
,其中a=﹣2. 粤公网安备 44130202000953号
粤公网安备 44130202000953号