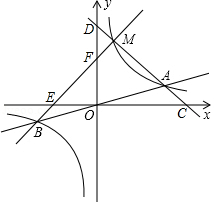
如图,函数 为常数, 的图象与过原点的 的直线相交于 , 两点,点 是第一象限内双曲线上的动点(点 在点 的左侧),直线 分别交 轴, 轴于 , 两点,连接 分别交 轴, 轴于点 , .现有以下四个结论:
① 与 的面积相等;②若 于点 ,则 ;③若 点的横坐标为1, 为等边三角形,则 ;④若 ,则 .
其中正确的结论的序号是 .(只填序号)
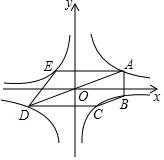
如图,经过原点 的直线与反比例函数 的图象交于 , 两点(点 在第一象限),点 , , 在反比例函数 的图象上, 轴, 轴,五边形 的面积为56,四边形 的面积为32,则 的值为 , 的值为 .
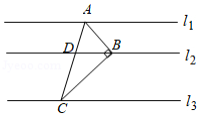
如图,直线 , , , 分别为直线 , , 上的动点,连接 , , ,线段 交直线 于点 .设直线 , 之间的距离为 ,直线 , 之间的距离为 ,若 , ,且 ,则 的最大值为 .
如图,矩形 中, ,将矩形 绕点 顺时针旋转 ,点 、 分别落在点 、 处.如果点 、 、 在同一条直线上,那么 的值为 .

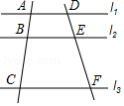
如图,直线 ,直线 交 , , 于点 , , ;直线 交 , , 于点 , , ,已知 ,则 .
小丽在"红色研学"活动中深受革命先烈事迹的鼓舞,用正方形纸片制作成图1的七巧板,设计拼成图2的"奔跑者"形象来激励自己.已知图1正方形纸片的边长为4,图2中 ,则"奔跑者"两脚之间的跨度,即 , 之间的距离是 .
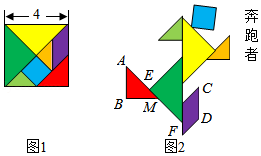
图1是一个闭合时的夹子,图2是该夹子的主视示意图,夹子两边为 , (点 与点 重合),点 是夹子转轴位置, 于点 , 于点 , , , , .按图示方式用手指按夹子,夹子两边绕点 转动.
(1)当 , 两点的距离最大时,以点 , , , 为顶点的四边形的周长是 .
(2)当夹子的开口最大(即点 与点 重合)时, , 两点的距离为 .