如图, 的直径 , 为 上的动点,连结 , 为 的中点,若点 在圆上运动一周,则点 经过的路径长是 .

如图,放置在直线 上的扇形 .由图①滚动(无滑动)到图②,再由图②滚动到图③.若半径 , ,则点 所经过的运动路径的长是
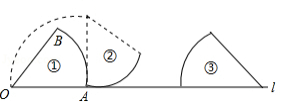
A. B. C. D.
如图,点 的坐标是 , ,点 是以 为直径的 上一动点,点 关于点 的对称点为 .当点 在 上运动时,所有这样的点 组成的图形与直线 有且只有一个公共点,则 的值等于 .

如图, 中, , , ,点 是 边上一点且 ,点 是线段 上一动点,连接 ,以 为斜边在 的下方作等腰 .当 从点 出发运动至点 停止时,点 的运动路径长为 .

阅读理解:在平面直角坐标系中,若两点 、 的坐标分别是 , 、
, ,则 、 这两点间的距离为 .如 , ,则 .
对于某种几何图形给出如下定义:符合一定条件的动点形成的图形,叫做符合这个条件的点的轨迹.如平面内到线段两个端点距离相等的点的轨迹是这条线段的垂直平分线.
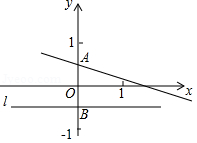
解决问题:如图,已知在平面直角坐标系 中,直线 交 轴于点 ,点 关于 轴的对称点为点 ,过点 作直线 平行于 轴.
(1)到点 的距离等于线段 长度的点的轨迹是 ;
(2)若动点 满足到直线 的距离等于线段 的长度,求动点 轨迹的函数表达式;
问题拓展:(3)若(2)中的动点 的轨迹与直线 交于 、 两点,分别过 、 作直线 的垂线,垂足分别是 、 ,求证:
① 是 外接圆的切线;
② 为定值.
如图,等腰 中,斜边 的长为2, 为 的中点, 为 边上的动点, 交 于点 , 为 的中点,当点 从点 运动到点 时,点 所经过的路线长为
A. B. C.1D.2
如图,在 中, , 在 内自由移动,若 的半径为1,且圆心 在 内所能到达的区域的面积为 ,则 的周长为 .

如图,在矩形 中, , ,点 是对角线 上的一个动点,连接 ,以 为斜边作 的直角三角形 ,使点 和点 位于 两侧,点 从点 到点 的运动过程中,点 的运动路径长是 .
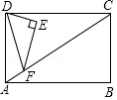
木杆 斜靠在墙壁上,当木杆的上端 沿墙壁 竖直下滑时,木杆的底端 也随之沿着射线 方向滑动.下列图中用虚线画出木杆中点 随之下落的路线,其中正确的是
A.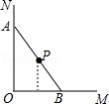 B.
B.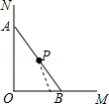
C.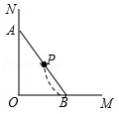 D.
D.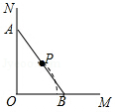
阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
问题:如图1,已知 为 的中位线, 是边 上一动点,连接 交 于点 ,那么动点 为线段 中点.
理由: 线段 为 的中位线, ,
由平行线分线段成比例得:动点 为线段 中点.
由此你得到动点 的运动轨迹是: .
知识应用:
如图2,已知 为等边 边 、 上的动点,连接 ;若 ,且等边 的边长为8,求线段 中点 的运动轨迹的长.
拓展提高:
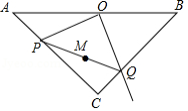
如图3, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连接 、 ,交点为 .
(1)求 的度数;
(2)若 ,求动点 运动轨迹的长.
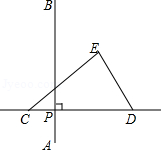
在 中, , , .如图,将直角顶点 放在原点,点 放在 轴正半轴上,当点 在 轴上向右移动时,点 也随之在 轴上向下移动,当点 到达原点时,点 停止移动,在移动过程中,点 到原点的最大距离为 .
在 中, , , .如图,将直角顶点 放在原点,点 放在 轴正半轴上,当点 在 轴上向右移动时,点 也随之在 轴上向下移动,当点 到达原点时,点 停止移动,在移动过程中,点 到原点的最大距离为 .
如图,在平面内,线段 , 为线段 上的动点,三角形纸片 的边 所在的直线与线段 垂直相交于点 ,且满足 .若点 沿 方向从点 运动到点 ,则点 运动的路径长为 .