初中数学命题与定理试题

命题：“如果 $m$是整数，那么它是有理数”，则它的逆命题为：　　．

对于命题“若 $a^2>b^2$，则 $a>b$”，下面四组关于 $a$， $b$的值中，能说明这个命题是假命题的是 $($　　 $)$

A． $a=3$， $b=2$B． $a=-3$， $b=2$C． $a=3$， $b=-1$D． $a=-1$， $b=3$

下列关于函数 $y=x^2-6x+10$的四个命题：

①当 $x=0$时， $y$有最小值10；

② $n$为任意实数， $x=3+n$时的函数值大于 $x=3-n$时的函数值；

③若 $n>3$，且 $n$是整数，当 $n⩽x⩽n+1$时， $y$的整数值有 $(2n-4)$个；

④若函数图象过点 $(a,y_0)$和 $(b,y_0+1)$，其中 $a>0$， $b>0$，则 $a<b$．

其中真命题的序号是 $($　　 $)$

A．①B．②C．③D．④

下列命题是真命题的是 $($　　 $)$

A．三个角相等的平行四边形是矩形

B．对角线相等的四边形是矩形

C．平行四边形的对角线互相垂直

D．对角线互相垂直的四边形是菱形

如图， $\mathit{AB}$是 $\odot O$的直径， $\mathit{AC}$， $\mathit{BC}$分别与 $\odot O$相交于点 $D$， $E$，连接 $\mathit{DE}$，现给出两个命题：

①若 $\mathit{AC}=\mathit{AB}$，则 $\mathit{DE}=\mathit{CE}$；

②若 $\angle C=45°$，记 $\mathit{\Delta CDE}$的面积为 $S_1$，四边形 $\mathit{DABE}$的面积为 $S_2$，则 $S_1=S_2$，

那么 $($　　 $)$

A．①是真命题 ②是假命题B．①是假命题 ②是真命题

C．①是假命题 ②是假命题D．①是真命题 ②是真命题

下列说法中，正确的是 $($　　 $)$

A．两条直线被第三条直线所截，内错角相等

B．对角线相等的平行四边形是正方形

C．相等的角是对顶角

D．角平分线上的点到角两边的距离相等

定义：若点 $P(a,b)$在函数 $y=\frac{1}{x}$的图象上，将以 $a$为二次项系数， $b$为一次项系数构造的二次函数 $y=a{x}^2+\mathit{bx}$称为函数 $y=\frac{1}{x}$的一个“派生函数”．例如：点 $(2,\frac{1}{2})$在函数 $y=\frac{1}{x}$的图象上，则函数 $y=2x^2+\frac{1}{2}x$称为函数 $y=\frac{1}{x}$的一个“派生函数”．现给出以下两个命题：

（1）存在函数 $y=\frac{1}{x}$的一个“派生函数”，其图象的对称轴在 $y$轴的右侧

（2）函数 $y=\frac{1}{x}$的所有“派生函数”，的图象都经过同一点，下列判断正确的是 $($　　 $)$

A．命题（1）与命题（2）都是真命题

B．命题（1）与命题（2）都是假命题

C．命题（1）是假命题，命题（2）是真命题

D．命题（1）是真命题，命题（2）是假命题

下列命题是真命题的是 $($　　 $)$

A．对角线相等的四边形是矩形

B．对角线互相垂直的四边形是菱形

C．任意多边形的内角和为 $360°$

D．三角形的中位线平行于第三边，并且等于第三边的一半

下列命题为真命题的是 $($　　 $)$

A．两条直线被一组平行线所截，所得的对应线段成比例

B．相似三角形面积之比等于相似比

C．对角线互相垂直的四边形是菱形

D．顺次连接矩形各边的中点所得的四边形是正方形

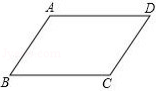
平行四边形的其中一个判定定理是：两组对边分别相等的四边形是平行四边形．请你证明这个判定定理．

已知：如图，在四边形 $\mathit{ABCD}$中， $\mathit{AB}=\mathit{CD}$， $\mathit{AD}=\mathit{BC}$．

求证：四边形 $\mathit{ABCD}$是平行四边形．

证明：

已知命题“关于 $x$的一元二次方程 $x^2+\mathit{bx}+1=0$，必有实数解”是假命题，则在下列选项中， $b$的值可以是 $($　　 $)$

A． $b=-3$B． $b=-2$C． $b=-1$D． $b=2$

下列命题为真命题的是 $($　　 $)$

A．有公共顶点的两个角是对顶角

B．多项式 $x^2-4x$因式分解的结果是 $x(x^2-4)$

C． $a+a=a^2$

D．一元二次方程 $x^2-x+2=0$无实数根

下列命题是假命题的是 $($　　 $)$

A．正五边形的内角和为 $540°$

B．矩形的对角线相等

C．对角线互相垂直的四边形是菱形

D．圆内接四边形的对角互补

以下命题是假命题的是 $($ 　　 $)$

A．	$\sqrt{4}$ 的算术平方根是2
B．	有两边相等的三角形是等腰三角形
C．	一组数据：3， $-1$ ，1，1，2，4的中位数是1.5
D．	过直线外一点有且只有一条直线与已知直线平行

下列说法正确的是 $($　　 $)$

①平行四边形既是中心对称图形，又是轴对称图形；②同一物体的三视图中，俯视图与左视图的宽相等；③线段的正投影是一条线段；④主视图是正三角形的圆锥的侧面展开图一定是半圆；⑤图形平移的方向总是水平的，图形旋转后的效果总是不同的．

A．①③B．②④C．③⑤D．②⑤