已知下列命题:
①若 a 3> b 3,则 a 2> b 2;
②若点 A( x 1, y 1)和点 B( x 2, y 2)在二次函数 y= x 2﹣2 x﹣1的图象上,且满足 x 1< x 2<1,则 y 1> y 2>﹣2;
③在同一平面内, a, b, c是直线,且 a∥ b, b⊥ c,则 a∥ c;
④周长相等的所有等腰直角三角形全等.
其中真命题的个数是( )
| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
下列命题中,真命题是
A.对角线互相垂直的梯形是等腰梯形
B.对角线互相垂直的平行四边形是正方形
C.对角线平分一组对角的平行四边形是菱形
D.对角线平分一组对角的梯形是直角梯形
下列命题中,假命题有( )
①两点之间线段最短;
②到角的两边距离相等的点在角的平分线上;
③过一点有且只有一条直线与已知直线平行;
④垂直于同一直线的两条直线平行;
⑤若⊙ O的弦 AB, CD交于点 P,则 PA• PB= PC• PD.
| A. |
4个 |
B. |
3个 |
C. |
2个 |
D. |
1个 |
下列命题中真命题是
A. 一定成立
B.位似图形不可能全等
C.正多边形都是轴对称图形
D.圆锥的主视图一定是等边三角形
下列说法中正确的是( )
| A. |
8的立方根是±2 |
| B. |
是一个最简二次根式 |
| C. |
函数y= 的自变量x的取值范围是x>1 |
| D. |
在平面直角坐标系中,点P(2,3)与点Q(﹣2,3)关于y轴对称 |
以下四个命题:
①任意三角形的一条中位线与第三边上的中线互相平分;
② , , , , , 六个足球队进行单循环赛,若 , , , , 分别赛了5,4,3,2,1场,则由此可知,还没有与 队比赛的球队可能是 队;
③两个正六边形一定位似;
④有13人参加捐款,其中小王的捐款数比13人捐款的平均数多2元,则小王的捐款数不可能最少,但可能只比最少的多,比其他的都少.
其中真命题的个数有
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
下列命题是假命题的是
A.若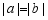 ,则
,则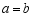
B.两直线平行,同位角相等
C.对顶角相等
D.若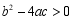 ,则方程
,则方程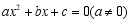 有两个不等的实数根
有两个不等的实数根
下列命题,其中是真命题的为
A.一组对边平行,另一组对边相等的四边形是平行四边形
B.对角线互相垂直的四边形是菱形
C.对角线相等的四边形是矩形
D.一组邻边相等的矩形是正方形
下列命题是假命题的是
A . 不在同一直线上的三点确定一个圆
B . 角平分线上的点到角两边的距离相等
C . 正六边形的内角和是
D . 角的边越大, 角就越大
下列说法正确的是
①平行四边形既是中心对称图形,又是轴对称图形;②同一物体的三视图中,俯视图与左视图的宽相等;③线段的正投影是一条线段;④主视图是正三角形的圆锥的侧面展开图一定是半圆;⑤图形平移的方向总是水平的,图形旋转后的效果总是不同的.
A.①③B.②④C.③⑤D.②⑤
如图, 是 的直径, , 分别与 相交于点 , ,连接 ,现给出两个命题:
①若 ,则 ;
②若 ,记 的面积为 ,四边形 的面积为 ,则 ,
那么

A.①是真命题 ②是假命题B.①是假命题 ②是真命题
C.①是假命题 ②是假命题D.①是真命题 ②是真命题
下列命题为真命题的是
A.有公共顶点的两个角是对顶角
B.多项式 因式分解的结果是
C.
D.一元二次方程 无实数根
定理:三角形的一个外角等于与它不相邻的两个内角的和.
已知:如图, 是 的外角.求证: .
| 证法1:如图, (三角形内角和定理), 又 (平角定义), (等量代换). (等式性质). |
| 证法2:如图, , , 且 (量角器测量所得) 又 (计算所得) (等量代换). |
下列说法正确的是

| A. |
证法1还需证明其他形状的三角形,该定理的证明才完整 |
| B. |
证法1用严谨的推理证明了该定理 |
| C. |
证法2用特殊到一般法证明了该定理 |
| D. |
证法2只要测量够一百个三角形进行验证,就能证明该定理 |
下列命题中:
①如果 ,那么
②一组对边平行,另一组对边相等的四边形是平行四边形
③从圆外一点可以引圆的两条切线,它们的切线长相等
④关于 的一元二次方程 有实数根,则 的取值范围是
其中真命题的个数是
A.1B.2C.3D.4