以下四个命题:
①任意三角形的一条中位线与第三边上的中线互相平分;
② , , , , , 六个足球队进行单循环赛,若 , , , , 分别赛了5,4,3,2,1场,则由此可知,还没有与 队比赛的球队可能是 队;
③两个正六边形一定位似;
④有13人参加捐款,其中小王的捐款数比13人捐款的平均数多2元,则小王的捐款数不可能最少,但可能只比最少的多,比其他的都少.
其中真命题的个数有
| A. |
1个 |
B. |
2个 |
C. |
3个 |
D. |
4个 |
相关知识点
推荐套卷
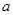 元提高50%标价,又以8折优惠卖出,则这种服装每件的售价是()
元提高50%标价,又以8折优惠卖出,则这种服装每件的售价是()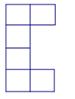
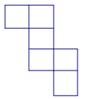
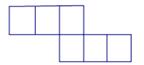
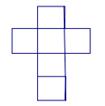

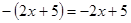
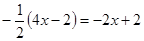
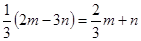
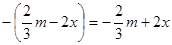
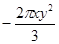 的系数和次数分别是 ()
的系数和次数分别是 ()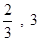
 粤公网安备 44130202000953号
粤公网安备 44130202000953号