初中数学命题与定理选择题

下列命题是假命题的是 $($　　 $)$

A ． 不在同一直线上的三点确定一个圆

B ． 角平分线上的点到角两边的距离相等

C ． 正六边形的内角和是 $720°$

D ． 角的边越大， 角就越大

下列命题正确的是 $($ 　　 $)$

A．	A ． 平行四边形的对角线互相垂直平分
B．	B ． 矩形的对角线互相垂直平分
C．	C ． 菱形的对角线互相平分且相等
D．	D ． 正方形的对角线互相垂直平分

下列命题中，假命题是 $($ 　　 $)$

A．	矩形的对角线相等
B．	矩形对角线交点到四个顶点的距离相等
C．	矩形的对角线互相平分
D．	矩形对角线交点到四条边的距离相等

下列说法正确的是 $($　　 $)$

①平行四边形既是中心对称图形，又是轴对称图形；②同一物体的三视图中，俯视图与左视图的宽相等；③线段的正投影是一条线段；④主视图是正三角形的圆锥的侧面展开图一定是半圆；⑤图形平移的方向总是水平的，图形旋转后的效果总是不同的．

A．①③B．②④C．③⑤D．②⑤

如图， $\mathit{AB}$是 $\odot O$的直径， $\mathit{AC}$， $\mathit{BC}$分别与 $\odot O$相交于点 $D$， $E$，连接 $\mathit{DE}$，现给出两个命题：

①若 $\mathit{AC}=\mathit{AB}$，则 $\mathit{DE}=\mathit{CE}$；

②若 $\angle C=45°$，记 $\mathit{\Delta CDE}$的面积为 $S_1$，四边形 $\mathit{DABE}$的面积为 $S_2$，则 $S_1=S_2$，

那么 $($　　 $)$

A．①是真命题 ②是假命题B．①是假命题 ②是真命题

C．①是假命题 ②是假命题D．①是真命题 ②是真命题

用三个不等式 $a>b$ ， $\mathit{ab}>0$ ， $\frac{1}{a}<\frac{1}{b}$ 中的两个不等式作为题设，余下的一个不等式作为结论组成一个命题，组成真命题的个数为 $($ 　　 $)$

A．

0

B．

1

C．

2

D．

3

下列命题为真命题的是 $($　　 $)$

A．有公共顶点的两个角是对顶角

B．多项式 $x^2-4x$因式分解的结果是 $x(x^2-4)$

C． $a+a=a^2$

D．一元二次方程 $x^2-x+2=0$无实数根

下列选项中，可以用来证明命题“若＞1，则a＞1”是假命题的反例是（   ）

A．a=﹣2

B．a=﹣1

C．a=1

D．a=2

定理：三角形的一个外角等于与它不相邻的两个内角的和．

已知：如图， $\angle \mathit{ACD}$ 是 $\mathit{\Delta ABC}$ 的外角．求证： $\angle \mathit{ACD}=\angle A+\angle B$ ．

证法1：如图， $\because \angle A+\angle B+\angle \mathit{ACB}=180°$ （三角形内角和定理）， 又     $\because \angle \mathit{ACD}+\angle \mathit{ACB}=180°$ （平角定义）， $\therefore \angle \mathit{ACD}+\angle \mathit{ACB}=\angle A+\angle B+\angle \mathit{ACB}$ （等量代换）． $\therefore \angle \mathit{ACD}=\angle A+\angle B$ （等式性质）．

证法2：如图， $\because \angle A=76°$ ，     $\angle B=59°$ ， 且     $\angle \mathit{ACD}=135°$ （量角器测量所得） 又     $\because 135°=76°+59°$ （计算所得） $\therefore \angle \mathit{ACD}=\angle A+\angle B$ （等量代换）．

下列说法正确的是 $($ 　　 $)$

A．	证法1还需证明其他形状的三角形，该定理的证明才完整
B．	证法1用严谨的推理证明了该定理
C．	证法2用特殊到一般法证明了该定理
D．	证法2只要测量够一百个三角形进行验证，就能证明该定理

下列命题中：

①如果 $a>b$，那么 $a^2>b^2$

②一组对边平行，另一组对边相等的四边形是平行四边形

③从圆外一点可以引圆的两条切线，它们的切线长相等

④关于 $x$的一元二次方程 $a{x}^2+2x+1=0$有实数根，则 $a$的取值范围是 $a⩽1$

其中真命题的个数是 $($　　 $)$

A．1B．2C．3D．4

下列语句正确的是 $($　　 $)$

A．对角线互相垂直的四边形是菱形

B．有两边及一角对应相等的两个三角形全等

C．矩形的对角线相等

D．平行四边形是轴对称图形

下列命题中，假命题的个数为（   ）
（1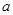）“是任意实数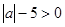，”是必然事件，
（2）抛物线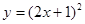的对称轴是直线，
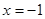（3）若某运动员投篮2次，投中1次，则该运动员投1次篮，投中的概率为，
（4）某件事情发生的概率是1，则它一定发生，
（5）某彩票的中奖率为10%，则买100张彩票一定有1张会中奖，
（6）函数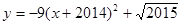与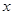轴必有两个交点．

A．2

B．3

C．4

D．5

下列命题的逆命题一定成立的是（  ）
①对顶角相等；
②同位角相等，两直线平行；
③若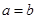，则；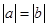
④若x=3，则．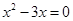

A．①②③

B．①④

C．②④

D．②

已知命题“关于 $x$的一元二次方程 $x^2+\mathit{bx}+1=0$，必有实数解”是假命题，则在下列选项中， $b$的值可以是 $($　　 $)$

A． $b=-3$B． $b=-2$C． $b=-1$D． $b=2$

下列四个命题中，其正确命题的个数是 $($　　 $)$

①若 $a>b$，则 $\frac{a}{c}>\frac{b}{c}$； ②垂直于弦的直径平分弦；③平行四边形的对角线互相平分；④反比例函数 $y=\frac{k}{x}$，当 $k<0$时， $y$随 $x$的增大而增大．

A．1B．2C．3D．4