如图,在 中, 为 的直径, 与 相切于点 ,与 相交于点 ,已知 , ,则 的长为 .

阅读理解:如图1, 与直线 、 都相切,不论 如何转动,直线 、 之间的距离始终保持不变(等于 的直径),我们把具有这一特性的图形称为“等宽曲线”,图2是利用圆的这一特性的例子,将等直径的圆棍放在物体下面,通过圆棍滚动,用较小的力就可以推动物体前进,据说,古埃及人就是利用这样的方法将巨石推到金字塔顶的.
拓展应用:如图3所示的弧三角形(也称为莱洛三角形)也是“等宽曲线”,如图4,夹在平行线 , 之间的莱洛三角形无论怎么滚动,平行线间的距离始终不变,若直线 , 之间的距离等于 ,则莱洛三角形的周长为 .

如图,在平面直角坐标系中,直线 的函数表达式为 ,点 的坐标为 ,以 为圆心, 为半径画圆,交直线 于点 ,交 轴正半轴于点 ,以 为圆心, 为半径画圆,交直线 于点 ,交 轴正半轴于点 ,以 为圆心, 为半径画圆,交直线 于点 ,交 轴正半轴于点 ; 按此做法进行下去,其中 的长为 .

如图,边长为1的正三角形 放置在边长为2的正方形内部,顶点 在正方形的一个顶点上,边 在正方形的一边上,将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第1次无滑动滚动(如图 ;再将 绕点 顺时针旋转,当点 落在正方形的边上时,完成第2次无滑动滚动(如图 , ,每次旋转的角度都不大于 ,依次这样操作下去,当完成第2016次无滑动滚动时,点 经过的路径总长为 .
如图,在 中,以 为直径的 分别与 , 相交于点 , , ,过点 作 的切线交边 于点 .
(1)求证: ;
(2)若 的半径为5, ,求 的长(结果保留 .

如图,在 中, ,点 是 边长一点, ,垂足为点 ,点 在线段 的延长线上,且 经过 , 两点.
(1)判断直线 与 的位置关系,并说明理由;
(2)若 的半径为2, 的长为 ,请求出 的度数.
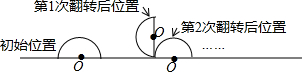
小明将量角器在桌面上进行连续翻转,如图为第1次、第2次翻转,若量角器的半径为1,则第2016次翻转后圆心 所走过的路径长为 .
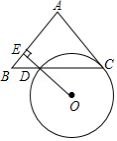
如图, 是半圆 的直径,点 是半圆上一点,连接 , ,以点 为顶点, 为边作 ,延长 交 于点 .
(1)求证:直线 是半圆 的切线;
(2)若 , ,求 的长.
如图,在 中,以 为直径的 与 相交于点 ,过点 作 的切线交 于点 .若 的半径为5, ,则 的长为 .

阅读理解:
我们把满足某种条件的所有点所组成的图形,叫做符合这个条件的点的轨迹.
例如:角的平分线是到角的两边距离相等的点的轨迹.
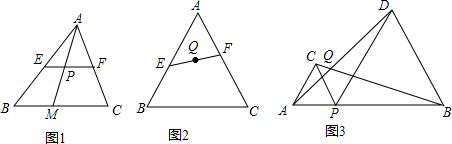
问题:如图1,已知 为 的中位线, 是边 上一动点,连接 交 于点 ,那么动点 为线段 中点.
理由: 线段 为 的中位线, ,
由平行线分线段成比例得:动点 为线段 中点.
由此你得到动点 的运动轨迹是: .
知识应用:
如图2,已知 为等边 边 、 上的动点,连接 ;若 ,且等边 的边长为8,求线段 中点 的运动轨迹的长.
拓展提高:
如图3, 为线段 上一动点(点 不与点 、 重合),在线段 的同侧分别作等边 和等边 ,连接 、 ,交点为 .
(1)求 的度数;
(2)若 ,求动点 运动轨迹的长.
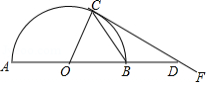
如图, 内接于 , 是直径, ,在 的内部作 ,且 ,过点 作 于点 ,连接 .
(1)若 交 于点 , 的半径是4,求 的长;
(2)请判断直线 与 的位置关系,并说明理由.
