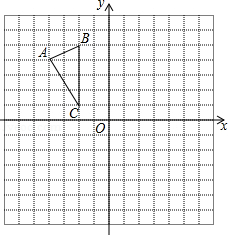
如图, 在平面直角坐标系内,顶点的坐标分别为 , , .
(1)平移 ,使点 移到点 ,画出平移后的△ ,并写出点 , 的坐标;
(2)将 绕点 旋转 ,得到△ ,画出旋转后的△ ;
(3)求(2)中的点 旋转到点 时,点 经过的路径长(结果保留 .
如图,在 中,以点 为圆心, 长为半径的圆恰好与 相切于点 ,交 于点 ,若 的长为 ,则 的半径为 .

如图,在平面直角坐标系中,已知点 ,以点 为旋转中心,将点 逆时针旋转到点 的位置,则 的长为 .

如图, 是 的外接圆, 为直径, 的平分线交 于点 ,过点 作 分别交 、 的延长线于点 、 .
(1)求证: 是 的切线;
(2)若 , ,求 的长度.(结果保留
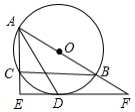
如图, 为等腰 的外接圆,直径 , 为弧 上任意一点(不与 , 重合),直线 交 延长线于点 , 在点 处切线 交 于点 ,下列结论正确的是 .(写出所有正确结论的序号)
①若 ,则弧 的长为 ;②若 ,则 平分 ;
③若 ,则 ;④无论点 在弧 上的位置如何变化, 为定值.

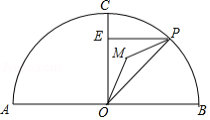
如图, 为 的直径,且 ,点 在半圆上, ,垂足为点 , 为半圆上任意一点(不与点 重合),过 点作 于点 ,设 的内心为 ,连接 、 .
(1)求 的度数;
(2)当点 在半圆上从点 运动到点 时,求内心 所经过的路径长.
如图,一块含有 角的直角三角板 ,在水平桌面上绕点 按顺时针方向旋转到 的位置,若 ,则顶点 从开始到结束所经过的路径长为 .
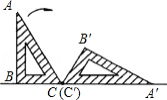
如图,半圆的圆心为 ,直径 的长为12, 为半圆上一点, , 的长是

A. B. C. D.
如图,半圆的圆心为 ,直径 的长为12, 为半圆上一点, , 的长是
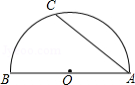
A. B. C. D.
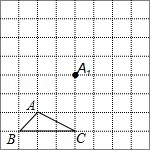
如图所示,正方形网格中, 为格点三角形(即三角形的顶点都在格点上)
①把 沿 方向平移,请在网格中画出当点 移动到点 时的△ ;
②把△ 绕点 按逆时针方向旋转 后得到△ ,如果网格中小正方形的边长为1,求点 旋转到 的路径长.
如图, 是 的内接三角形, 为 直径, , 平分 ,交 于点 ,交 于点 ,连接 .
(1)求证: ;
(2)若 ,求 的长(结果保留 .

如图,在 中, , ,将 绕点 按顺时针方向旋转到△ 的位置,点 刚好落在 的延长线上,求点 从开始到结束所经过的路径长为(结果保留 .
