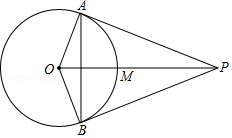
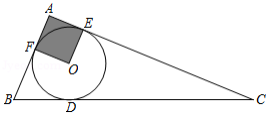
如图,已知 , 是 的两条切线, , 为切点,线段 交 于点 .给出下列四种说法:
① ;
② ;
③四边形 有外接圆;
④ 是 外接圆的圆心.
其中正确说法的个数是
| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图, 、 为圆 的切线,切点分别为 、 , 交 于点 , 的延长线交圆 于点 .下列结论不一定成立的是

| A. |
为等腰三角形 |
| B. |
与 相互垂直平分 |
| C. |
点 、 都在以 为直径的圆上 |
| D. |
为 的边 上的中线 |
如图,在中,以
为直径的
交
于点
,连接
,且
,连接
并延长交
的延长线于点
,
与
相切于点
.
(1)求证:是
的切线;
(2)连接交
于点
,求证:
;
(3)若,求
的值.

如图, 、 为圆 的切线,切点分别为 、 , 交 于点 , 的延长线交圆 于点 ,下列结论不一定成立的是

| A. |
|
B. |
|
C. |
|
D. |
平分 |
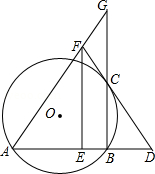
如图,顶点为的抛物线
与
轴交于
,
两点,与
轴交于点
.
(1)求这条抛物线对应的函数表达式;
(2)问在轴上是否存在一点
,使得
为直角三角形?若存在,求出点
的坐标;若不存在,说明理由.
(3)若在第一象限的抛物线下方有一动点,满足
,过
作
轴于点
,设
的内心为
,试求
的最小值.
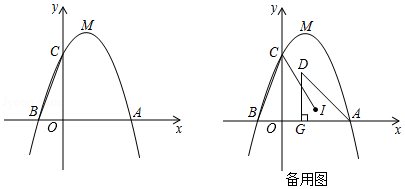
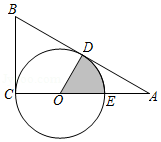
如图,为
直角边
上一点,以
为半径的
与斜边
相切于点
,交
于点
,已知
,
.则图中阴影部分的面积是 .
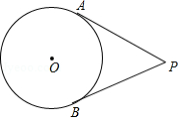
如图, 为圆 外一点, , 分别切圆 于 , 两点,若 ,则
| A. |
2 |
B. |
3 |
C. |
4 |
D. |
5 |
如图, 的内切圆 与 、 、 分别相切于点 、 、 ,且 , , ,则阴影部分(即四边形 的面积是
| A. |
4 |
B. |
6.25 |
C. |
7.5 |
D. |
9 |
如图, 已知: 是 的弦, 过点 作 交 于点 ,过点 作 的切线交 的延长线于点 ,取 的中点 ,过点 作 交 的延长线于点 ,连接 并延长交 的延长线于点 .
求证:
(1) ;
(2) .
如图,是
的直径,过
外一点
作
的两条切线
,
,切点分别为
,
,连接
,
.
(1)求证:;
(2)连接,
,若
,
,
,求
的长.

(年贵州省黔东南州)如图,已知PC平分∠MPN,点O是PC上任意一点,PM与⊙O相切于点E,交PC于A、B两点.
(1)求证:PN与⊙O相切;
(2)如果∠MPC=30°,PE= ,求劣弧
,求劣弧 的长.
的长.
(年新疆、生产建设兵团)如图1,一个圆球放置在V型架中.图2是它的平面示意图,CA、CB都是⊙O的切线,切点分别是A、B,如果⊙O的半径为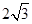 cm,且AB=6cm,求∠ACB.
cm,且AB=6cm,求∠ACB.