初中数学圆内接四边形的性质试题

在边长为1的小正方形组成的方格纸中，若多边形的各顶点都在方格纸的格点（横竖格子线的交错点）上，这样的多边形称为格点多边形．记格点多边形内的格点数为a，边界上的格点数为b，则格点多边形的面积可表示为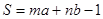，其中m，n为常数．

（1）在下面的方格中各画出一个面积为6的格点多边形，依次为三角形、平行四边形（非菱形）、菱形；
（2）利用（1）中的格点多边形确定m，n的值．

如图，正方形ABCD的边长为4+2，点E在对角线BD上，且∠BAE=，EF⊥AB，垂足为点F，则EF的长是           

在平面直角坐标系O中，过原点O及点A(0，2) 、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D 点P从点O出发，以每秒个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动 设移动时间为t秒，当t为      时，△PQB为直角三角形。

分别以□ABCD（∠CDA≠90°）的三边AB，CD，DA为斜边作等腰直角三角形，△ABE，△CDG，△ADF．

（1）如图1，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF．请判断GF与EF的数量关系及位置关系；（只写结论，不需证明）
（2）如图2，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，（1）中结论还成立吗？若成立，给出证明；若不成立，说明理由．

如图，已知在正方形ABCD中，点O为对角线AC的中点，过O点的射线OM、ON分别交AB、BC于点E、F，且∠EOF=90°，BO、EF交于点P，则下面结论中：①图形中全等的三角形只有三对；②△EOF是等腰直角三角形；③正方形ABCD的面积等于四边形OEBF面积的4倍；④BE+BF=OA；⑤+
=2OP·OB.正确结论的个数是（    ）

A.4个      B.3个        C.2个       D.1个

如图，AD是△ABC的角平分线，DE⊥AC，垂足为E，BF∥AC交ED的延长线于点F，若BC恰好平分∠ABF，AE=2BF．给出下列四个结论：①DE=DF；②DB=DC；③AD⊥BC；④AC=3BF，其中正确的结论共有（ ）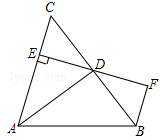

A．4个

B．3个

C．2个

D．1个

如图，在菱形ABCD中，对角线AC，BD相交于点O，AC=12，BD=16，E为AD中点，点P在x轴上移动．若△POE为等腰三角形，请写出所有符合要求的点P的坐标                ．

我国汉代数学家赵爽为了证明勾股定理，创制了一幅“弦图”，后人称其为“赵爽弦图”（如图（1）），图（2）由弦图变化得到，它是由八个全等的直角三角形拼接而成，记图中正方形ABCD、正方形EFGH、正方形MNKT的面积分别为、、．若正方形EFGH的边长为2，则=      ．

如图，在边长为10的菱形ABCD中，对角线BD ="16." 点E是AB的中点，P、Q是BD上的动点，且始终保持PQ ="2." 则四边形AEPQ周长的最小值为_________．（结果保留根号）

如图，已知△ABC，直线PQ垂直平分AC，与边AB交于E，连接CE，过点C作CF平行于BA交PQ于点F，连接AF．

（1）求证：△AED≌△CFD；
（2）求证：四边形AECF是菱形．
（3）若AD=3，AE=5，则菱形AECF的面积是多少？

（本题14分）已知，在△ABC中，∠BAC=90°，∠ABC=45°，点D为直线BC上一动点（点D不与点B，C重合）．以AD为边做正方形ADEF，连接CF．
（1）如图1当点D在线段BC上时．求证：CF+CD=BC；
（2）如图2，当点D在线段BC的延长线上时，其他条件不变，请直接写出CF，BC，CD三条线段之间的关系；
（3）如图3，当点D在线段BC的反向延长线上时，且点A，F分别在直线BC的两侧，其他条件不变；
①请直接写出CF，BC，CD三条线段之间的关系；
②若正方形ADEF的边长为2，对角线AE，DF相交于点O，连接OC，求OC的长度．

如图，在平行四边形ABCD中，E、F为BC上两点，且BE=CF,AF=DE.

（1）找出图中一对全等的三角形，并证明；
（2）求证：四边形ABCD是矩形．

如图，用纸折出黄金分割点：裁一张正方的纸片ABCD，先折出BC的中点E，再折出线段AE，然后通过折叠使EB落到线段EA上，折出点B的新位置B′，因而EB′=EB．类似地，在AB上折出点B″使AB″=AB′．这时B″就是AB的黄金分割点．请你证明这个结论．

如图，矩形ABCD的对角线AC=10，BC=8，则图中五个小矩形的周长之和为_______．

如图①，在□ABCD中，AB＝13，BC＝50，点P从点B出发，沿B—A—D—A运动．已知沿B—A运动时的速度为每秒13个单位长度，沿A—D—A运动时的速度为每秒8个单位长度．点Q从点 B出发沿BC方向运动，速度为每秒5个单位长度. 若P、Q两点同时出发，当点Q到达点C时，P、Q两点同时停止运动．设点P的运动时间为t（秒）．连结PQ．

（1）当点P沿A—D—A运动时，求AP的长（用含t的代数式表示）．
（2）过点Q作QR//AB，交AD于点R，连结BR，如图②．在点P沿B—A—D运动过程中，是否存在线段PQ扫过的图形（阴影部分）被线段BR分成面积相等的两部分的情况，若存在，求出所有t的值，若不存在，请说明理由．
（3）设点C.D关于直线PQ的对称点分别为、，在点P沿B—A—D运动过程中， 当//BC时，求t的值（直接写出结果）．