初中数学圆内接四边形的性质试题

在平面直角坐标系x、y中，过原点O及点A（0，2）、C（6，0）作矩形OABC，∠AOC的平分线交AB于点D．点P从点O出发，以每秒个单位长度的速度沿射线OD方向移动；同时点Q从点O出发，以每秒2个单位长度的速度沿x轴正方向移动．设移动时间为t秒．

（1）当点P移动到点D时，求出此时t的值；
（2）当t为何值时，△PQB为直角三角形；
（3）已知过O、P、Q三点的抛物线解析式为（t＞0）．问是否存在某一时刻t，将△PQB绕某点旋转180°后，三个对应顶点恰好都落在上述抛物线上？若存在，求出t的值；若不存在，请说明理由．

如图，在菱形ABCD中，边长为10，∠A=60°．顺次连结菱形ABCD各边中点，可得四边形A₁B₁C₁D₁；顺次连结四边形A₁B₁C₁D₁各边中点，可得四边形A₂B₂C₂D₂；顺次连结四边形A₂B₂C₂D₂各边中点，可得四边形A₃B₃C₃D₃；按此规律继续下去…．则四边形A₂B₂C₂D₂的周长是　   　；四边形A₂₀₁₃B₂₀₁₃C₂₀₁₃D₂₀₁₃的周长是　   　．

如图，正方形ABCD的边长为4，P为正方形边上一动点，沿A→D→C→B→A 的路径匀速移动，设P点经过的路径长为x，△APD的面积是y，则下列图象能大致反映y与x的函数关系的是

A．	B．
C．	D．

如图．在边长为6的正方形 $\mathit{ABCD}$中，点 $E$， $F$分别在 $\mathit{BC}$， $\mathit{CD}$上， $\mathit{BC}=3\mathit{BE}$且 $\mathit{BE}=\mathit{CF}$， $\mathit{AE}\perp \mathit{BF}$，垂足为 $G$， $O$是对角线 $\mathit{BD}$的中点，连接 $\mathit{OG}$、则 $\mathit{OG}$的长为 　　．

如图所示，在直角梯形ABCD中，AD//BC，∠A＝90°，AB＝12，BC＝21，AD=16。动点P从点B出发，沿射线BC的方向以每秒2个单位长的速度运动，动点Q同时从点A出发，在线段AD上以每秒1个单位长的速度向点D运动，当其中一个动点到达端点时另一个动点也随之停止运动。设运动的时间为t（秒）。

（1）设△DPQ的面积为S，用含有t的代数式表示S。
（2）当t为何值时，四边形PCDQ是平行四边形？

如图1所示，将一个边长为2的正方形ABCD和一个长为2、宽为1的长方形CEFD拼在一起，构成一个大的长方形ABEF.现将小长方形CEFD绕点C顺时针旋转至,旋转角为.

（1）当点恰好落在EF边上时，求旋转角的值；
（2）如图2，G为BC的中点，且0⁰＜＜90⁰，求证：；
（3）小长方形CEFD绕点C顺时针旋转一周的过程中，与能否全等？若能，直接写出旋转角的值；若不能，说明理由.

如图，在四边形ABCD中，AB=BC，对角线BD平分ÐABC，P是BD上一点，过点P作PM^AD，PN^CD，垂足分别为M、N。

（1）求证：ÐADB=ÐCDB；
（2）若ÐADC=90°，求证：四边形MPND是正方形。

设边长为3的正方形的对角线长为a，下列关于a的四种说法：① a是无理数；② a可以用数轴上的一个点来表示；③ 3<a<4；④ a是18的算术平方根。其中，所有正确说法的序号是

A．①④

B．②③

C．①②④

D．①③④

（本小题满分9分）如图1，已知B点坐标是（6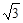，6），BA⊥x轴于A，BC⊥y轴于C，D在线段OA上，E在y轴的正半轴上,DE⊥BD，M是DE中点，且M在OB上．

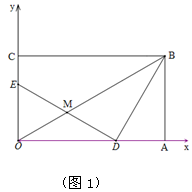
（1）点M的坐标是（        ，        ），DE=        ；
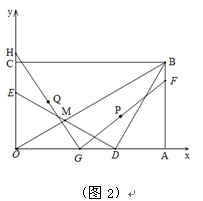
（2）小明在研究动点问题时发现，如果有两点分别在两条互相垂直的直线上做匀速运动，连接这两点所得线段的中点将在同一条直线上运动，利用这一事实解答下列问题，如图2，如果一动点F从点B出发以每秒1个单位长度的速度向点A运动，同时有一点G从点D出发以每秒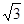个单位长度的速度向点O运动，点H从点E开始沿y轴正方向自由滑动，并始终保持GH=DE,P为FG的中点，Q为GH的中点,F与G两个点分别运动到各自终点时停止运动，分别求出在运动过程中点P、Q运动的路线长．
（3）连接PQ，求当运动多少秒时，PQ最小，最小值是多少？

如图，矩形ABCD中，AB=4，BC=3，边CD在直线L上，将矩形ABCD沿直线L作无滑动翻滚，当点A第一次翻滚到点A₁位置时，则点A经过的路线长为       .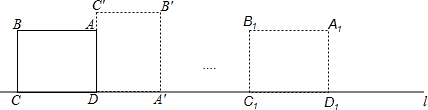

如图，在等腰梯形ABCD中，已知AD//BC，AB=DC，AC与BD交于点O，廷长BC到E，使得CE=AD，连接DE。
（1）求证：BD=DE。
（2）若AC⊥BD，AD=3，S_ABCD=16，求AB的长。

如图，在ABCD中，F是AD的中点，延长BC到点E，使CE=BC，连结DE，CF。

（1）求证：四边形CEDF是平行四边形；
（2）若AB=4，AD=6，∠B=60°，求DE的长。

如图，E是矩形ABCE的边BC上一点，EF⊥AE，EF分别交AC、CD于点M、F，BG⊥AC，垂足为G，BG交AE于点H。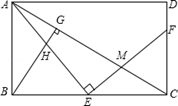

（1）求证：△ABE∽△ECF；
（2）找出与△ABH相似的三角形，并证明；
（3）若E是BC中点，BC=2AB，AB=2，求EM的长。

如图，□ABCD中，E是AB中点，F在AD上，且AF＝FD，EF交AC于G，则AG︰AC＝______．

如图，正方形ABCD的对角线相交于点O，∠CAB的平分线分别交BD、BC于点E、F，作BH⊥AF于点H，交AC于点G，连接GE、GF．

（1）求证：△OAE≌△OBG；
（2）求证：四边形BFGE是菱形．