分别以□ABCD（∠CDA≠90°）的三边AB，CD，DA为斜边作等腰直角三角形，△ABE，△CDG，△ADF．
（1）如图1，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF．请判断GF与EF的数量关系及位置关系；（只写结论，不需证明）
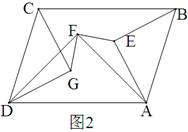
（2）如图2，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，（1）中结论还成立吗？若成立，给出证明；若不成立，说明理由．
+2)÷
，其中
，
.
；（2）
；（2）
相关知识点
推荐套卷
分别以□ABCD（∠CDA≠90°）的三边AB，CD，DA为斜边作等腰直角三角形，△ABE，△CDG，△ADF．
（1）如图1，当三个等腰直角三角形都在该平行四边形外部时，连接GF，EF．请判断GF与EF的数量关系及位置关系；（只写结论，不需证明）
（2）如图2，当三个等腰直角三角形都在该平行四边形内部时，连接GF，EF，（1）中结论还成立吗？若成立，给出证明；若不成立，说明理由．
粤公网安备 44130202000953号