初中数学圆内接四边形的性质解答题

如图，把含有30°角的三角板ABO置入平面直角坐标系中，A，B两点坐标分别为（3，0）和（0，3）．动点P从A点开始沿折线AO－OB－BA运动，点P在AO，OB，BA上运动的面四民﹒数学兴趣小组对捐款情况进行了抽样调查，速度分别为1，，2 （长度单位/秒）﹒一直尺的上边缘l从x轴的位置开始以（长度单位/秒）的速度向上平行移动（即移动过程中保持l∥x轴），且分别与OB，AB交于E，F两点﹒设动点P与动直线l同时出发，运动时间为t秒，当点P沿折线AO－OB－BA运动一周时，直线l和动点P同时停止运动．

请解答下列问题：
（1）过A，B两点的直线解析式是   ；
（2）当t﹦4时，点P的坐标为    ；当t ﹦    ，点P与点E重合；
（3）① 作点P关于直线EF的对称点P′．在运动过程中，若形成的四边形PEP′F为菱形，则t的值是多少？② 当t﹦2时，是否存在着点Q，使得△FEQ ∽△BEP ?若存在, 求出点Q的坐标；若不存在，请说明理由．

我们知道平行四边形有很多性质。现在如果我们把平行四边形沿着它的一条对角线翻折。会发现这其中还有更多的结论，如图，已知平行四边形ABCD中，∠B＝30º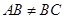，，将△ABC沿AC翻折至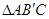，连接。
【发现与证明】：如图1：求证：①△AGC是等腰三角形；
②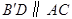（只选一个证明哟，4分）
【应用与解答】：如图2：如果AB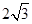＝，BC＝1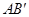，与CD相交于点E，求△AEC的面积
【拓展与探索】如果AB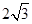＝，当BC的长为多少时，△AB′D是直角三角形？

在平面直角坐标系xOy中，直线分别与x轴，y轴交于过点A，B，点C是第一象限内的一点，且AB=AC，AB⊥AC，抛物线经过A，C两点，与轴的另一交点为D．
（1）求此抛物线的解析式；
（2）判断直线AB与CD的位置关系，并证明你的结论；
（3）点M为x轴上一动点，在抛物线上是否存在一点N，使以A,B,M,N四点构成的四边形为平行四边形？若存在，求点N的坐标；若不存在，请说明理由．

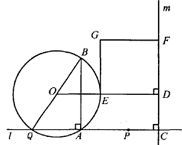
（本题14分）如图，点A和动点P在直线上，点P关于点A的对称点为Q，以AQ为边作Rt△ABQ，使∠BAQ=90°，AQ:AB=3:4，作△ABQ的外接圆O。点C在点P右侧，PC=4，过点C作直线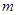⊥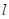，过点O作OD⊥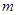于点D，交AB右侧的圆弧于点E。在射线CD上取点F，使DF=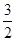CD，以DE，DF为邻边作矩形DEGF，设AQ=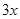

（1）用关于的代数式表示BQ，DF；
（2）当点P在点A右侧时，若矩形DEGF的面积等于90，求AP的长；
（3）在点P的整个运动过程中，
①当AP为何值时，矩形DEGF是正方形？
②作直线BG交⊙O于另一点N，若BN的弦心距为1，求AP的长（直接写出答案）

（本小题满分14分）如图，四边形OMTN中，OM=ON，TM=TN，我们把这种两组邻边分别相等的四边形叫做筝形.

（1）试探究筝形对角线之间的位置关系，并证明你的结论；
（2）在筝形ABCD中，已知AB=AD=5，BC=CD，BC>AB，BD，AC为对角线，BD=8.
①是否存在一个圆使得A，B，C，D四个点都在这个圆上？若存在，求出圆的半径；若不存在， 请说明理由；
②过点B作BF⊥CD，垂足为F，BF交AC于点E，连接DE.当四边形ABED为菱形时，求点F到AB 的距离.

（本小题12分） 菱形ABCD的边长为2，∠BAD＝60°，对角线AC，BD相交于点O，动点P在线段AC上从点A向点C运动，过P作PE∥AD，交AB于点E，过P作PF∥AB，交AD于点F，四边形QHCK与四边形PEAF关于直线BD对称. 设菱形ABCD被这两个四边形盖住部分的面积为S₁，AP＝x：

（1）对角线AC的长为     ；S_菱形ABCD＝     ；
（2）用含x的代数式表示S₁；
（3）设点P在移动过程中所得两个四边形PEAF与QHCK的重叠部分面积为S₂，当S₂＝S_菱形ABCD时，求x的值．

已知直角坐标系中菱形ABCD的位置如图所示，C．D两点的坐标分别为 （4，0）、（0，3）．现有两动点P、Q分别从A、C同时出发，点P沿线段AD向终点D运动，点Q沿折线CBA向终点A运动，设运动时间为ts．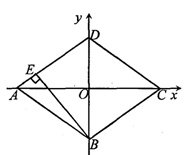

（1）菱形ABCD的边长是   ，面积是   ， 高BE的长是   ．（直接填写结果）
（2）探究下列问题：
①若点P的速度为1cm/s，点Q的速度为2 cm/s．当点Q在线段BA上时，求△APQ的面积S关于t的函数关系式，以及S的最大值；
②若点P的速度为1cm/s，点Q的速度变为kcm/s，在运动过程中，任何时刻都有相应的k值，使得△APQ沿它的一边翻折，翻折前后两个三角形组成的四边形为菱形，请探究当t＝4s时的情形，并求出k的值．

如图，在锐角三角形纸片ABC中，AC＞BC，点D，E，F分别在边AB，BC，CA上．

（1）已知：DE∥AC，DF∥BC．
①判断
四边形DECF一定是什么形状？并说明理由．
②裁剪
当AC=24cm，BC=20cm，∠ACB=45°时，请你探索：如何剪四边形DECF，能使它的面积最大，并证明你的结论；
（2）折叠
请你只用两次折叠，确定四边形的顶点D，E，C，F，使它恰好为菱形，并说明你的折法和理由．

在□ABCD中，点E、F分别在AB、CD上，且AE=CF．
（1）求证：△ADE≌△CBF；
（2）若DF=BF，求证：四边形DEBF为菱形．

如图，等腰梯形ABCD中，AB＝CD，AD∥BC，点E、F在BC上，且BE＝CF．

（1）求证：AE＝DF；
（2）若AD＝EF，试证明四边形AEFD为矩形．

已知矩形纸片ABCD中，AB=24厘米，BC=10厘米．

（1）按如下操作：先将矩形纸片上下对折，而后左右对折，再沿对角线对折，而后展开得到图中的折痕四边形EFGH（如图1），求菱形EFGH的面积．
（2）如图2，将矩形纸片ABCD折叠，使点A与点C重合得折痕EF，则四边形AECF必为菱形，请加以证明．
（3）请通过一定的操作，构造一个菱形EFGH（不同于第（1）题中的特殊图形），使菱形的四个顶点分别落在矩形ABCD的四条边上（E、F、G、H分别在边AB、BC、CD、DA上，且不与矩形ABCD的顶点重合）．
①请简述操作的方法，并在图3中画出菱形EFGH．
②求菱形EFGH的面积的取值范围．

如图①，②在矩形ABCD中，将矩形折叠，使B落在边AD（含端点）上，落点记为E，这时折痕与边BC或者边CD（含端点）交于F，然后展开铺平，则以B、E、F为顶点的三角形△BEF称为矩形ABCD的“折痕三角形”
（1）由“折痕三角形”的定义可知，矩形ABCD的任意一个“折痕△BEF”是一个     三角形。
（2）如图③，在矩形ABCD中，AB=2，BC=4，，当它的“折痕△BEF”的顶点E位于AD的中点时，画出这个“折痕△BEF”，并求出点F的坐标；
（3）如图④，在矩形ABCD中，AB=2，BC=4，该矩形是否存在面积最大的“折痕△BEF”？若存在，说明理由，并求出此时点E的坐标？若不存在，为什么？
 
          

如图，矩形ABCD的边AB=3cm，AD=4cm，点E从点A出发，沿射线AD移动，以CE为直径作圆O，点F为圆O与射线BD的公共点，连接EF、CF，过点E作EG⊥EF，EG与圆O相交于点G，连接CG．

（1）试说明四边形EFCG是矩形；
（2）当圆O与射线BD相切时，点E停止移动，在点E移动的过程中，
①矩形EFCG的面积是否存在最大值或最小值？若存在，求出这个最大值或最小值；若不存在，说明理由；
②求点G移动路线的长．

已知矩形OABC中，OA=3，AB=6，以OA、OC所在的直线为坐标轴，建立如图所示的平面直角坐标系。将矩形OABC绕点O顺时针方向旋转，得到矩形ODEF，当点B在直线DE上时，设直线DE和轴交于点P，与轴交于点Q．

（1）求证：△BCQ≌△ODQ；
（2）求点P的坐标；

如图，在矩形ABCD中，AB=6cm，BC=8cm．如果点E由点B出发沿BC方
向向点C匀速运动，同时点F由点D出发沿DA方向向点A匀速运动，它们的速度分别为2cm/s和1cm/s．FQ⊥BC，分别交AC、BC于点P和Q，设运动时间为t（s）（0＜t＜4）．

（1）连结EF、DQ，若四边形EQDF为平行四边形，求t的值；
（2）连结EP，设△EPC的面积为ycm²，求y与t的函数关系式，并求y的最大值；