初中数学圆内接四边形的性质选择题

菱形具有而矩形不一定具有的性质是                               (    )

A．对角线互相垂直

B．对角线相等

C．对角线互相平分

D．对角互补

若顺次连接四边形ABCD各边的中点所得四边形是菱形．则四边形ABCD一定是 (   )

A．茭形	B．对角线互相垂直的四边形
C．矩形	D．对角线相等的四边形

如图，矩形ABCD中，AB＜BC，对角线AC、BD相交于点O，则图中的等腰三角形有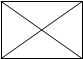

A．2个            B．4个            C．6个            D．8个

如图（二）所示，在□ABCD中，对角线AC、BD相交于点O，且AB≠AD，则下列式子不正确的是
A．AC⊥BD           B．AB＝CD           C．BO＝OD           D．∠BAD＝∠BCD

如图，在矩形ABCD中，AB=3，BC=4，点P在BC上运动，连结DP，过点A作AE⊥DP，垂足为E．设DP=x，AE=y，则能反映y与x之间函数关系的大致图象是（   ）.

 

如图，在□ABCD中，E是BC的中点，且∠AEC=∠DCE，则下列结论不正确的


是（    ）.

A．	B．BF=DF
C．四边形AECD是等腰梯形	D．∠AEB=∠ADC

如图，在直角梯形ABCD中，∠ABC=90^o，DC∥AB，BC=3，DC=4，AD=5．动点P从B点出发，由B→C→D→A沿边运动，则△ABP的最大面积为（　　）.

A．10

B．12

C．14

D．16

菱形ABCD中, AE⊥BC于E, 交BD于F点, 下列结论:
①BF为∠ABE的角平分线; ②DF＝2BF;
③2AB²=DF·DB;   ④sin∠BAE=.
其中正确的为                                    （　　）
A. ②③   B. ①②④        C. ①③④        C. ①④

若一个多边形的每个外角都等于，则它的边数是

A．6

B．7

C．8

D．9

如图，中，AB=10，BC=6，E、F分别是AD、DC的中点，若EF=7，则四边形EACF的周长是

A．20          B．22         C．29          D．31

如图，中，AB=10，BC=6，E、F分别是AD、DC的中点，若EF=7，则四边形EACF的周长是

A．20          B．22         C．29          D．31

已知菱形的边长和一条对角线的长均为2cm，则菱形的面积为(　　)

在下列命题中，是真命题的是(　　)

A．两条对角线相等的四边形是矩形

B．两条对角线互相垂直且相等的四边形是正方形

C．两条对角线互相垂直的四边形是菱形

D．两条对角线互相平分的四边形是平行四边形

如图，两条宽度都为1的纸条，交叉重叠放在一起，且它们的交角为α，则它们重叠部分（图中阻影部分）的面积为（   ）

A．

B．

C．

D．1

图，正方形中，为的中点，于，交于点，交于点，连接、。有如下结论：①；②；③；④；⑤。其中正确的结论的个数为（ ）

A．2个

B．3个

C．4个

D．5个