初中数学圆内接四边形的性质选择题

（11·柳州）如图，在平行四边形ABCD中，EF∥AD，HN∥AB，则图中的平行四边形的个数共有

A．12个

B．9个

C．7个

D．5个

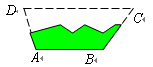
（11·柳州）如图，阴影部分是一块梯形铁片的残余部分，量得∠A＝100º，∠B＝115º，则梯形另外两个底角的度数分别是

A．100º、115º

B．100º、65º

C．80º、115º

D．80º、65º

如图，△ABC和△ADE都是等腰直角三角形，∠BAC=∠DAE=90°，四边形ACDE是平行四边形，连结CE交AD于点F，连结BD交CE于点G，连结BE. 下列结论中：① CE=BD；       ②△ADC是等腰直角三角形；
③∠ADB=∠AEB； ④ CD·AE=EF·CG；
一定正确的结论有

A．1个

B．2个

C．3个

D．4个

如图，在梯形ABCD中，AB∥CD，AD＝BC，点E，F，G，H分别是AB，BC，CD，DA的中点，则下列结论一定正确的是（■）.

A．∠HGF＝∠GHE	B．∠GHE＝∠HEF
C．∠HEF＝∠EFG	D．∠HGF＝∠HEF

如图，△ABC和△CDE均为等腰直角三角形，点B，C，D在一条直线上，点M是AE的中点，下列结论：①tan∠AEC=；②S_△ABC+S_△CDE≥S_△ACE；③BM⊥DM；④BM=DM．正确结论的个数是（　　）

A．1个	B．2个
C．3个	D．4个

如图，矩形ABCD申，对角线AC、BD相交于点0，∠AOB=60⁰，AB=5，则AD的长是（  )．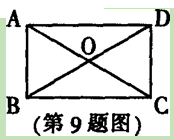

（A)5    （B）5  （C）5    (D)10

正多边形的一个内角为135°，则该多边形的边数为

A．9

B．8

C．7

D．4

正方形纸片折一次，沿折痕剪开，能剪得的图形是

A．锐角三角形

B．钝角三角形

C．梯形

D．菱形

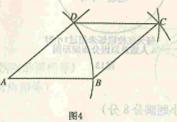
（11·西宁）用直尺和圆规作一个菱形，如图4，能得到四边形ABCD是菱形的依据是

A．一组邻边相等的四边形是菱形	B．四边都相等的四边形是菱形
C．对角线互相垂直的平行四边形是菱形	D．每条对角线平分一组对角的平行四边形是菱形

（11·西宁）用直尺和圆规作一个菱形，如图4，能得到四边形ABCD是菱形的依据是

A．一组邻边相等的四边形是菱形	B．四边都相等的四边形是菱形
C．对角线互相垂直的平行四边形是菱形	D．每条对角线平分一组对角的平行四边形是菱形

（11·台州）在梯形ABCD中，AD∥BC，∠ABC＝90º，对角线AC、BD相交于
点O．下列条件中，不能判断对角线互相垂直的是【   】
A．∠1＝∠2          B．∠1＝∠3
C．∠2＝∠3          D．OB²＋OC²＝BC²

如图，把一张矩形纸片ABCD沿对角线BD折叠，使点C落
在E处，BE与AD相交于F，下列结论：①BD²＝AD²+AB²
②△ABF≌△EDF ③④AD=BD·cos45°正确的是（  ）

A．①②

B．②③

C．①④

D．③④

如图，把一张矩形纸片ABCD沿对角线BD折叠，使点C落
在E处，BE与AD相交于F，下列结论：①BD²＝AD²+AB²
②△ABF≌△EDF ③④AD=BD·cos45°正确的是（  ）

A．①②

B．②③

C．①④

D．③④

在一个四边形ABCD中，依次连结各边中点的四边形是菱形，则对角线AC与BD需要满足条件                                                            （    ）
A. 垂直          B. 相等             C.垂直且相等      D. 不再需要条件

如图：矩形ABCD的对角线AC＝10，BC＝8，则图中五个小矩形的周长之和为

A．14

B．16

C．20

D．28