初中数学圆内接四边形的性质试题

如图，在平面直角坐标系中有一矩形ABCO，B点的坐标为（12，6），点C、A在坐标轴上．⊙A、⊙P的半径均为1，点P从点C开始在线段CO上以1单位/秒的速度向左运动，运动到点O处停止．与此同时，⊙A的半径每秒钟增大2个单位，当点P停止运动时，⊙A的半径也停止变化．设点P运动的时间为t秒．
在0＜t＜12时，设△OAP的面积为s，试求s与t的函数关系式．并求出当t为何值时，s为矩形ABCO面积的；
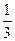在点P的运动过程中，是否存在某一时刻，⊙A与⊙P相切，若存在求出点P的坐标，若不存在，说明理由．

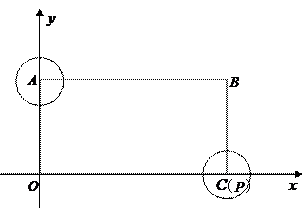
如图，△ABC中，已知∠BAC＝45°，AD⊥BC于D，BD＝4㎝，DC＝6㎝，试求AD的长. 小萍同学灵活运用轴对称知识，将图形进行翻折变换，巧妙地解答了此题。请按照小萍的思路，探究并解答下列问题：
分别以AB、AC所在的直线为对称轴，画出△ABD、△ACD的轴对称图形，D点的对称点分别为点E、F，延长EB、FC相交于G点，试证明四边形AEGF是正方形；
设AD＝x㎝,联系(1)的结论，试求出AD的长；

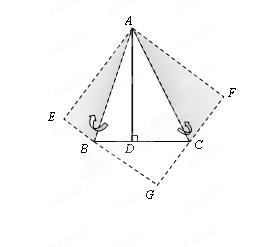
如图，菱形ABCD的对角线长分别为，以菱形ABCD各边的中点为顶点作矩形A₁B₁C₁D₁，然后再以矩形A₁B₁C₁D₁的中点为顶点作菱形A₂B₂C₂D₂，……，如此下去，得到四边形A₂₀₁₁B₂₀₁₁C₂₀₁₁D₂₀₁₁的面积用含的代数式表示为         ____。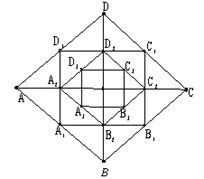

在直角梯形ABCD中，AB∥DC，AB⊥BC，∠A＝60°，AB＝2CD，E、F分别为AB、AD的中点，连结EF、EC、BF、CF.

判断四边形AECD的形状（不证明）；
在不添加其它条件下，写出图中一对全等的三角形，用符号“≌”表示，并证明。
若CD＝2，求梯形ABCD的面积。

如图，在梯形ABCD中，AB∥DC，DB平分∠ADC，过点A作AE∥BD，交CD的延长线于点E，且∠C＝2∠E．

（1）求证：梯形ABCD是等腰梯形．
（2）若∠BDC＝30°，AD＝5，求CD的长．

如图，已知BE⊥AD，CF⊥AD，且BE＝CF．
试判断AD是△ABC的中线还是角平分线？请证明你的结论．
连接BF、CE，若四边形BFCE是菱形，则△ABC中应添加的一个条件是          

如图，把一张矩形纸片ABCD沿对角线BD对折，使点C落在点E处，BE与AD交于点F.试判断重合部分图形的形状，并说明理由.

如图，四边形ABCD是菱形，DE⊥AB交BA的延长线于E，DF⊥BC，交BC的延长线于F．
求证：DE=DF

如图，在矩形ABCD中，对角线AC、BD相交于O，AB=OA=3，则BC=      .

如图，在梯形ABCD中，AD∥BC,E为BC上一点，DE∥AB,AD的长为1，BC的长为2，则CE的长为        .

命题“等腰梯形的对角线相等”.它的逆命题是                    .

如图，将一张一个角为60°的直角三角形纸片，沿其一条中线剪开后，不能拼成的四边形是（   ）.

A．邻边不等的矩形	B．等腰梯形
C．有一个角是锐角的菱形	D．正方形

如图，已知四边形ABCD是平行四边形，下列结论中不一定正确的是（   ）.

A．AB=CD	B．AB=AC
C．当AC⊥BD时，它是菱形
D．当∠ABC=90°时，它是矩形

在□ABCD中，E是AB延长线上的一点，若∠1=60°，则∠A的度数为（   ）.

A．120°

B．60°

C．45°

D．30°

如图，将长8cm，宽4cm的矩形纸片ABCD折叠，使点A与C  重合，则△CEB的面积为__      ___.