如图,已知以直角梯形ABCD的腰CD为直径的半圆O与梯形的上底AD、下底BC以及腰AB均相切,切点分别是D、C、E.若半圆O的半径为2,梯形的腰AB为5,则该梯形的周长是( ).
| A.9 | B.10 | C.12 | D.14 |
如图,在等腰梯形ABCD中,AB∥CD, 对角线AC⊥BC,∠B=60º,BC=2cm,则梯形ABCD的面积为( )

A.3 cm cm |
B.6 cm |
C.6 cm cm |
D.12 cm |
已知如图,矩形OABC的长OA=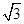 ,宽OC=1,
,宽OC=1,
将△AOC沿AC翻折得△APC.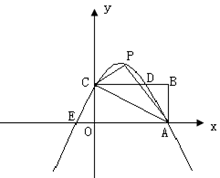
求∠PCB的度数
若P,A两点在抛物线y=-
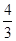 x2+bx+c上,求b,c的值,并 说明点C在此抛物线上;
x2+bx+c上,求b,c的值,并 说明点C在此抛物线上;(2)中的抛物线与矩形OABC边CB相交于点D,与x轴相交 于另外一点E,若点M是x轴上的点,N是y轴上的点,以点E、M、D、N为顶点的四边形是平行四边形,试求点M、N的坐标.
如图1,在 中,
中,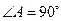 ,
,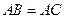 ,
,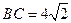 ,另有一等腰梯形
,另有一等腰梯形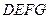 (
(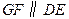 )的底边
)的底边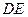 与
与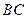 重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
重合,两腰分别落在AB、AC上,且G、F分别是AB、AC的中点.
直接写出△AGF与△ABC的面积的比值;
操作:固定
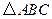 ,将等腰梯形
,将等腰梯形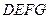 以每秒1个单位的速度沿
以每秒1个单位的速度沿 方向向右运动,直到点
方向向右运动,直到点 与点
与点 重合时停止.设运动时间为
重合时停止.设运动时间为 秒,运动后的等腰梯形为
秒,运动后的等腰梯形为 (如图2).
(如图2).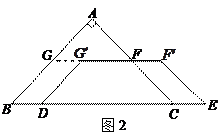
①探究1:在运动过程中,四边形 能否是菱形?若能,请求出此时
能否是菱形?若能,请求出此时 的值;若不能,请说明理由.
的值;若不能,请说明理由.
②探究2:设在运动过程中 与等腰梯形
与等腰梯形 重叠部分的面积为
重叠部分的面积为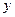 ,求
,求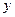 与
与 的函数关系式.
的函数关系式.
如图,在菱形ABCD中,AB=2cm,∠BAD=60°,E为CD边中点,点P从点A开始沿AC方向以每秒 cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
cm的速度运动,同时,点Q从点D出发沿DB方向以每秒1cm的速度运动,当点P到达点C时,P,Q同时停止运动,设运动的时间为x秒.
当点P在线段AO上运动时.
①请用含x的代数式表示OP的长度;
②若记四边形PBEQ的面积为y,求y关于x的函数关系式(不要求写出自变量的取值范围)显然,当x=0时,四边形PBEQ即梯形ABED,请问,当P在线段AC的其他位置时,以P,B,E,Q为顶点的四边形能否成为梯形?若能,求出所有满足条件的x的值;若不能,请说明理由.
已知:如图, 为正方形
为正方形 的对角线,
的对角线, 为
为 上一点,联结
上一点,联结 ,
, ,当
,当 时,
时, 的度数为( )
的度数为( )
| A.54° | B.27° |
| C.36° | D.18° |
如图1,在正方形铁皮上剪下一个扇形和一个半径为1cm的圆形,使之恰好围成图2所示的一个圆锥,则圆锥的高为【 】
| A.cm | B.4cm | C.cm | D.cm |
小明为今年将要参加中考的好友小李制作了一个(如图)正方体礼品盒,六面上各有一字,连起来就是“预祝中考成功”,其中“预”的对面是“中”,“成”的对面是“功”,则它的平面展开图可能是( )
如图, 过
过 上到点
上到点 的距离为1,3,5,7,…的点作
的距离为1,3,5,7,…的点作 的垂线,分别与
的垂线,分别与 相交,得到图所示的阴影梯形,它们的面积依次记为
相交,得到图所示的阴影梯形,它们的面积依次记为 ….则
….则
 ;
;通过计算可得
 .
.
如图, (甲)是四边形纸片ABCD,其中ÐB=120°,ÐD=50°。若将其右下角向内折出rPCR,恰使CP∥AB,RC∥AD,如图(乙)所示,则ÐC= °.