如图,在  中,
中,  是直径,
是直径,  是弦,
是弦,  ,垂足为
,垂足为  ,连接
,连接  ,
,  ,
,  ,则下列说法中正确的是
,则下列说法中正确的是 


| A. |
|
B. |
|
C. |
|
D. |
|
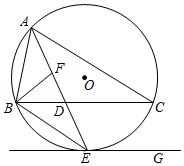
如图,已知⊙ O的半径为2, AB为直径, CD为弦. AB与 CD交于点 M,将 沿 CD翻折后,点 A与圆心 O重合,延长 OA至 P,使 AP= OA,连接 PC
(1)求 CD的长;
(2)求证: PC是⊙ O的切线;
(3)点 G为 的中点,在 PC延长线上有一动点 Q,连接 QG交 AB于点 E.交 于点 F( F与 B、 C不重合).问 GE• GF是否为定值?如果是,求出该定值;如果不是,请说明理由.

如图,以点 O为圆心的两个同心圆中,大圆的弦 AB是小圆的切线,点 P为切点, , OP=6,则劣弧 AB的长为 .

如图, 是 的外接圆,直线 与 相切于点 , ,连接 交 于点 .
(1)求证: 平分 ;
(2)若 的平分线 交 于点 ,且 , ,求 的长.
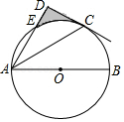
已知 为 的直径且长为 , 为 上异于 , 的点,若 与过点 的 的切线互相垂直,垂足为 .①若等腰三角形 的顶角为120度,则 ,②若 为正三角形,则 ,③若等腰三角形 的对称轴经过点 ,则 ,④无论点 在何处,将 沿 折叠,点 一定落在直径 上,其中正确结论的序号为 .
如图, 是 的直径, 是 的弦, 交 于点 ,连接 , ,过点 作 ,垂足为 , .
(1)求证: ;
(2)点 在 的延长线上,连接 , .
①求证: 与 相切;
②当 , 时,直接写出 的长.

四边形 内接于 , 是 的直径, .
(1)如图1,求证 ;
(2)过点 作 的切线,交 延长线于点 (如图 .若 , ,求 的长.

如图,在平面直角坐标系中,点 在第一象限, 与 轴、 轴都相切,且经过矩形 的顶点 ,与 相交于点 .若 的半径为5,点 的坐标是 .则点 的坐标是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,为
的直径,
为
上一点,
与过
点的直线互相垂直,垂足为
,
平分
.
(1)求证:为
的切线.
(2)若,
,求
的半径.

定义:对角线互相垂直且相等的四边形叫做垂等四边形.
(1)下面四边形是垂等四边形的是 ;(填序号)
①平行四边形;②矩形;③菱形;④正方形
(2)图形判定:如图1,在四边形 中, , ,过点 作 垂线交 的延长线于点 ,且 ,证明:四边形 是垂等四边形.
(3)由菱形面积公式易知性质:垂等四边形的面积等于两条对角线乘积的一半.应用:在图2中,面积为24的垂等四边形 内接于 中, .求 的半径.

如图,在四边形 中, , , ,过点 的 与边 , 分别交于 , 两点. ,垂足为 , .连接 , , .

(1)若 ,试判断 的形状,并说明理由;
(2)若 ,求证: 与 相切于点 .
如图, 是 的直径, , 是 上两点,且 ,连接 , .过点 作 交 的延长线于点 .
(1)判定直线 与 的位置关系,并说明理由;
(2)若 , ,求图中阴影部分的面积.