如图,在平面直角坐标系中,已知点 ,以点 为旋转中心,将点 逆时针旋转到点 的位置,则 的长为 .

如图,在 中, , , .按以下步骤作图:
①以 为圆心,任意长为半径作弧,分别交 , 于点 , ;
②分别以 , 为圆心,以大于 的长为半径作弧,两弧相交于点 ;
③作射线 ;
④以同样的方法作射线 .
交 于点 ,连接 ,则 .

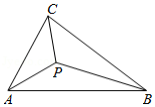
如图, 是 的内心,连接 、 、 , 、 、 的面积分别为 、 、 .则 .(填“ ”或“ ”或“ ”
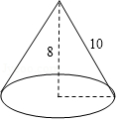
如图,圆锥的母线长为 ,高为 ,则该圆锥的侧面展开图(扇形)的弧长为 .(结果用 表示)
如图,已知 为 的直径,直线 经过点 ,且 , ,线段 和 分别交 于点 、 , ,则 .
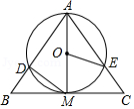
如图, 为等腰 的外接圆,直径 , 为弧 上任意一点(不与 , 重合),直线 交 延长线于点 , 在点 处切线 交 于点 ,下列结论正确的是 .(写出所有正确结论的序号)
①若 ,则弧 的长为 ;②若 ,则 平分 ;
③若 ,则 ;④无论点 在弧 上的位置如何变化, 为定值.

我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率 的近似值,设半径为 的圆内接正 边形的周长为 ,圆的直径为 ,如图所示,当 时, ,那么当 时, .(结果精确到0.01,参考数据:

如图,这是某同学用纸板做成的一个底面直径为 ,高为 的无底圆锥形玩具(接缝忽略不计),则做这个玩具所需纸板的面积是 (结果保留 .
