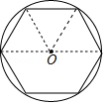
我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率 的近似值,设半径为 的圆内接正 边形的周长为 ,圆的直径为 ,如图所示,当 时, ,那么当 时, .(结果精确到0.01,参考数据:
推荐套卷
我国魏晋时期的数学家刘徽创立了“割圆术”,认为圆内接正多边形边数无限增加时,周长就越接近圆周长,由此求得了圆周率 的近似值,设半径为 的圆内接正 边形的周长为 ,圆的直径为 ,如图所示,当 时, ,那么当 时, .(结果精确到0.01,参考数据:
