初中数学圆解答题

证明题24．如图8，在  ABCD中，DE＝BF.

求证：四边形AFCE是平行四边形.

 

（11·湖州）（本小题10分）
如图，已知E、F分别是□ABCD的边BC、AD上的点，且BE=DF。
⑴求证：四边形AECF是平行四边形；
⑵若BC=10，∠BAC=90°，且四边形AECF是菱形，求BE的长。

数学课上，李老师出示了这样一道题目：如图，正方形的边长为，为边延长线上的一点，为的中点，的垂直平分线交边于，交边的延长线于.当时，与的比值是多少？
经过思考，小明展示了一种正确的解题思路：过作直线平行于交，分别于，，如图，则可得：，因为，所以.可求出和的值，进而可求得与的比值.
(1) 请按照小明的思路写出求解过程.
(2) 小东又对此题作了进一步探究，得出了的结论.你认为小东的这个结论正确吗？如果正确，请给予证明；如果不正确，请说明理由.

已知梯形ABCD中，AD∥BC，AB=AD（如图所示），∠BAD的平分线AE交BC于点E，连接DE．
（1）在下图中，用尺规作∠BAD的平分线AE（保留作图痕迹不写作法），并证明四边形ABED是菱形．
（2）若∠ABC=60°，EC=2BE．求证：ED⊥DC．

如图，点G是正方形ABCD对角线CA的延长线上任意一点，以线段AG为边作一个正方形AEFG，线段EB和GD相交于点H．
（1）求证：EB=GD；
（2）判断EB与GD的位置关系，并说明理由；
（3）若AB=2，AG=，求EB的长．

如图，正方形ABCD的四个顶点分别在四条平行线l₁、l₂、l₃、l₄上，这四条直
线中相邻两条之间的距离依次为h₁、h₂、h₃(h₁＞0，h₂＞0，h₃＞0)．
(1)求证：h₁＝h₂；
(2)设正方形ABCD的面积为S，求证：S＝(h₁＋h₂)²＋h₁²；
(3)若h₁＋h₂＝1，当h₁变化时，说明正方形ABCD的面积S随h₁的变化情况．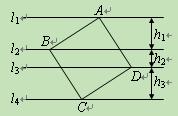

如图所示，在菱形ABCD中，∠ABC=60°，DE∥AC交BC的延长线于点E．

求证：DE=BE．

如图，矩形ABCD中，AB=6，BC=2，点O是AB的中点，点P在AB的延长线上，且BP=3．一动点E从O点出发，以每秒1个单位长度的速度沿OA匀速运动，到达A点后，立即以原速度沿AO返回；另一动点F从P点发发，以每秒1个单位长度的速度沿射线PA匀速运动，点E、F同时出发，当两点相遇时停止运动，在点E、F的运动过程中，以EF为边作等边△EFG，使△EFG和矩形ABCD在射线PA的同侧．设运动的时间为t秒（t≥0）．
（1）当等边△EFG的边FG恰好经过点C时，求运动时间t的值；
（2）在整个运动过程中，设等边△EFG和矩形ABCD重叠部分的面积为S，请直接写出S与t之间的函数关系式和相应的自变量t的取值范围；
（3）设EG与矩形ABCD的对角线AC的交点为H，是否存在这样的t，使△AOH是等腰三角形？若存大，求出对应的t的值；若不存在，请说明理由．

如图，梯形ABCD中，AD∥BC，∠DCB=45°，CD=2，BD⊥CD．过点C作CE⊥AB于E，交对角线BD于F，点G为BC中点，连接EG、AF．
（1）求EG的长；
（2）求证：CF=AB+AF．

图10是小红设计的钻石形商标，△ABC是边长为2的等边三角形，四边形ACDE是等腰梯形，AC∥ED，∠EAC=60°，AE=1．
（1）证明：△ABE≌△CBD；
（2）图中存在多对相似三角形，请你找出一对进行证明，并求出其相似比（不添加辅助线，不找全等的相似三角形）；
（3）小红发现AM=MN=NC，请证明此结论；
（4）求线段BD的长．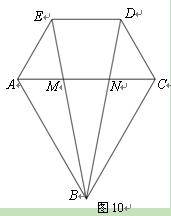

如图6，在梯形ABCD中，AB∥CD，AD =DC，求证：AC是∠DAB的平分线．

（本小题9分）如图10，在直角三角形ABC中，ÐACB=90°，AC=BC=10，将△
ABC绕点B沿顺时针方向旋转90°得到△A₁BC₁.
（1）线段A₁C₁的长度是             ，ÐCBA₁的度数是            .
（2）连结CC₁，求证：四边形CBA₁C₁是平行四边形.

（满分8分）如图，已知直线AB与轴交于点C，与双曲线交于A（3，
）、B（-5，）两点.AD⊥轴于点D，BE∥轴且与轴交于点E.
（1）求点B的坐标及直线AB的解析式；
（2）判断四边形CBED的形状，并说明理由.

如图，直角梯形纸片ABCD中，AD//BC，∠A=90º，∠C=30º．折叠纸片使BC经过点D，点C落在点E处，BF是折痕，且BF=CF=8．
（1）求∠BDF的度数；
（2）求AB的长．

如图，在ABCD中，∠DAB=60°，AB=2AD，点E、F分别是AB、CD的中点，过点A作AG∥BD，交CB的延长线于点G。
（1）求证：四边形DEBF是菱形；
（2）请判断四边形AGBD是什么特殊四边形？并加以证明。