初中数学圆选择题

如图，平行四边形 ABCD的周长为，AC、BD相交于点O，OE⊥AC交AD于E，则△DCE的周长为（   ）

A．4      B．6       C．8      D．10

下列说法中正确的是（    ）

A．两条对角线垂直的四边形是菱形

B．对角线垂直且相等的四边形是正方形

C．两条对角线相等的四边形是矩形

D．两条对角线相等的平行四边形是矩形

如图，在矩形ABCD中，AB=1，BC=2，将其折叠，使AB边落在对角线AC上，得到折痕AE，则点E到点B的距离为（    ）              

A．

B．

C．

D．

如图，▱ABCD的对角线AC、BD相交于点O，则下列说法一定正确的是（ ）

A．AO=OD      B．AO⊥OD      C．AO=OC      D．AO⊥AB

如图，以数轴的单位长度为边作一个正方形，以数轴的原点为圆心，正方形对角线长为半径画弧，交数轴正半轴于点A，则点A表示的数是（ ）

A．1

B．1.4

C．

D．

如图，在▱ABCD中，O是对角线AC，BD的交点，下列结论错误的是（ ）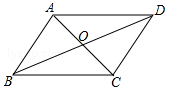

A．AB∥CD

B．AB=CD

C．AC=BD

D．OA=OC

关于四边形ABCD：
①两组对边分别相等；
②一组对边平行且相等；
③一组对边平行且另一组对边相等；
④两条对角线相等．以上四种条件中，
可以判定四边形ABCD是平行四边形的有（     ）．

A．①②③④

B．①③④

C．①②

D．③④

如图，已知在矩形ABCD中，AB=4，BC=2，点M，E在AD上，点F在边AB上，并且DM=1，现将△AEF沿着直线EF折叠，使点A落在边CD上的点P处，则当PB+PM的和最小时，ME的长度为（     ）

A．

B．

C．

D．

如图，菱形ABCD中，AB=2，∠A=120°，点P，Q，K分别为线段BC，CD，BD上的任意一点，则PK+QK的最小值为（ ）

A．1

B．

C．2

D．

一个多边形的每个外角都等于72°，则这个多边形的边数为（     ）

A．5

B．6

C．7

D．8

正方形具有菱形不一定具有的性质是（    ）

A．对角线互相垂直	B．对角线互相平分
C．对角线相等	D．对角线平分一组对角

下列命题，真命题（   ）

A．有两边相等的平行四边形是菱形

B．有一个角是直角的四边形是矩形

C．四个角相等的菱形是正方形

D．平分弦的直径垂直于这条弦

四边形ABCD的对角线AC、BD相较于点O，有下列条件①AB=AD；②；③AO="CO" BO=DO；④矩形ABCD；⑤菱形ABCD；⑥正方形ABCD，则下列推理中，不成立的是（  ）
A．①④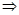⑥         B．①③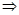⑤       C．①②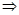⑥        D．②③④

一个多边形的内角和是360°，这个多边形是（ ）

A．三角形

B．四边形

C．六边形

D．不能确定

如图，矩形纸片ABCD，AB=3，AD=5，折叠纸片，使点A落在BC边上的E处，折痕为PQ，当点E在BC边上移动时，折痕的端点P、Q也随之移动．若限定点P、Q分别在AB、AD边上移动，则点E在BC边上可移动的最大距离为（ ）

A．1             B．2             C．4                 D．5