初中数学圆试题

将矩形纸片ABCD按如图所示的方式折叠，得到菱形AECF．若AB＝6，则BC的长为(    )

A．1

B．2

C．2

D．12

如图，在Rt△ABC中，∠BAC=90°，D、E分别是AB、BC的中点，F在CA的延长线上，∠FDA=∠B，AC=6，AB=8，则四边形AEDF的周长为（    ）

A．22            B．20             C．18             D．16

如图，矩形的面积为6，它的两条对角线交于点，以、为两邻边作平行四边形，平行四边形的对角线交于点，同样以、 为两邻边作平行四边形，……，依次类推，则平行四边形的面积为           .

已知边长为1的正方形ABCD中，点E、F分别在边BC、CD上，

（1）如图1，若AE⊥BF，求证：EA=FB；
（2）如图2，若∠EAF=, AE的长为，试求AF的长度。

如图，在梯形ABCD中，AD∥BC，E为BC的中点，BC＝2AD，EA＝ED＝2，AC与ED相交于点F.

(1)求证：梯形ABCD是等腰梯形；
(2)当AB与AC具有什么位置关系时，四边形AECD是菱形？请说明理由，并求出此时菱形AECD的面积．

如图，在梯形ABCD中，AB∥CD，AD＝BC，将△ACD沿对角线翻折后，点D恰好与边AB的中点M重合．

(1)点C是否在以AB为直径的圆上？请说明理由．
(2)当AB＝4时，求此梯形的面积．

如图，直角梯形OABC中，OC∥AB，C(0，3)，B(4，1)，以BC为直径的圆交x轴于D、E两点(点D在点E的右方)求点E、D的坐标．

如图，点D是△ABC的边AB的延长线上一点，点F是边BC上的一个动点(不与点B重合)，以BD、BF为邻边作平行四边形BDEF，又AP綊BE(点P、E在直线AB的同侧)，如果BD＝AB，那么△PBC的面积与△ABC的面积之比为(　　)

A.     B.    C.     D.

如图，在菱形ABCD中，E为AD中点，EF⊥AC交CB的延长线于F.求证：AB与EF互相平分.

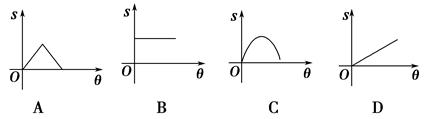
如图，两个边长相等的正方形ABCD和EFGH，正方形EFGH的顶点E固定在正方形ABCD的对称中心位置，正方形EFGH绕点E顺时针方向旋转，设它们重叠部分的面积为S，旋转的角度为θ，S与θ的函数关系的大致图象是（　　）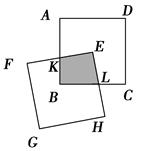

如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动（与A、C不重合），Q是CB延长线上一动点，与点P同时以相同的速度由B向CB延长线方向运动（Q不与B重合），过P作PE⊥AB于E，连接PQ交AB于D.

（1）当∠BQD＝30°时，求AP的长；
（2）在运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由.

如图，在平行四边形ABCD中，点E为AD的中点，连接BE，交AC于点F，则AF∶CF＝       ．

如图，矩形ABCD中，AB=6，第1次平移将矩形ABCD沿AB的方向向右平移5个单位，得到矩形A₁B₁C₁D₁，第2次平移将矩形A₁B₁C₁D₁沿A₁B₁的方向向右平移5个单位，得到矩形A₂B₂C₂D₂…，第n次平移将矩形A_n-1B_n-1C_n-1D_n-1沿A_n-1B_n-1的方向平移5个单位，得到矩形A_nB_nC_nD_n（n＞2）．

（1）求AB₁和AB₂的长．
（2）若AB_n的长为56，求n．

如图1，等腰直角三角板的一个锐角顶点与正方形ABCD的顶点A重合，将此三角板绕点A旋转，使三角板中该锐角的两条边分别交正方形的两边BC，DC于点E，F，连接EF．

（1）猜想BE、EF、DF三条线段之间的数量关系，并证明你的猜想；
（2）在图1中，过点A作AM⊥EF于点M，请直接写出AM和AB的数量关系；
（3）如图2，将Rt△ABC沿斜边AC翻折得到Rt△ADC，E，F分别是BC，CD边上的点，∠EAF=∠BAD，连接EF，过点A作AM⊥EF于点M，试猜想AM与AB之间的数量关系．并证明你的猜想．

已知，如图，AC为平行四边形ABCD的对角线，点E是边AD上一点，

（1）若∠CAD=∠EBC，AC=BE，AB=6，求CE的长。
（2）若AE+AB=BC,求证：∠BEC=∠ABE+∠BAD.