如图,在边长为2的菱形ABCD中,∠A=60°,M是AD边的中点,N是AB边上一动点,将△AMN沿MN所在的直线翻折得到△A′MN,连接A′C. 则A′C长度的最小值是 .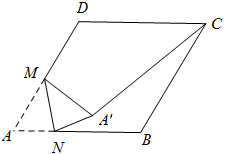
如图,在矩形 中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为( )
中,点A的坐标是(-2,1),点C的纵坐标是4,则B、C两点的坐标为( )
A.( ,
, )、(
)、( ,
, ) B.(
) B.( ,
, )、(
)、( ,
, )
)
C.( ,
, )、(
)、( ,
, ) D.(
) D.( ,
, ) 、(
) 、( ,
, )
)
如图,在Rt△ABC中,∠B=90°,AC=60,AB=30。点D是AC上的动点,过D作DF⊥BC于F,再过F作FE//AC,交AB于E。设CD=x,DF=y.
(1)求y与x的函数关系式;
(2)当四边形AEFD为菱形时,求x的值;
(3)当△FED是直角三角形时,求x的值.
如图1,正六边形ABCDEF的边长为a,P是BC边上一动点,过P作PM∥AB交AF于M,作PN∥CD交DE于N.
(1)①∠MPN= ;
②求证:PM+PN=3a;
(2)如图2,点O是AD的中点,连接OM、ON,求证:OM=ON;
(3)如图3,点O是AD的中点,OG平分∠MON,判断四边形OMGN是否为特殊四边形?并说明理由.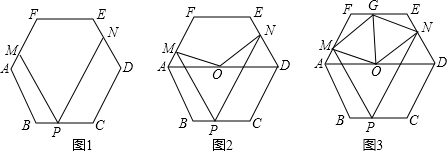
如图,已知⊙O的半径为1,DE是⊙O的直径,过点D作⊙O的切线AD,C是AD的中点,AE交⊙O于B点,四边形BCOE是平行四边形.
(1)求AD的长;
(2)BC是⊙O的切线吗?若是,给出证明;若不是,说明理由.
如图,正方形 的边长为2,以
的边长为2,以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;然后以
;然后以 为对角线作正方形
为对角线作正方形 ,又以
,又以 为圆心、
为圆心、 为半径作弧
为半径作弧 交
交 于点
于点 ,设弧
,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 ;…,按此规律继续作下去,设弧
;…,按此规律继续作下去,设弧 与边
与边 、
、 围成的阴影部分面积为
围成的阴影部分面积为 .则:(1)
.则:(1) = ;(2)
= ;(2) = .
= .
如图,在正方形ABCD内作一个等边三角形ABE,连接DE、CE,有如下结论:①图中除等边三角形ABE外,还有三个等腰三角形;②△ADE≌△BCE;③此图形既是中心对称图形也是轴对称图形;④△ABE的面积与正方形ABCD的面积比是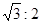 ;⑤△DEC与△ABE的面积比为
;⑤△DEC与△ABE的面积比为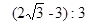 。则以上结论正确的是 .(只填正确结论的序号)
。则以上结论正确的是 .(只填正确结论的序号)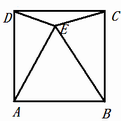
已知正方形ABCD的对角线AC与BD交于点O,点E、F分别是OB、OC上的动点,
(1)如果动点E、F满足BE=CF(如图):
①写出所有以点E或F为顶点的全等三角形(不得添加辅助线);
②证明:AE⊥BF;
(2)如果动点E、F满足BE=OF(如图),问当AE⊥BF时,点E在什么位置,并证明你的结论.
某校初四年级学习小组在探究学习过程中,用两块完全相同的且含60°角的直角三角板ABC与AFE按如图(1)所示位置放置,现将Rt△AEF绕A点按逆时针方向旋转角α(0°<α<90°),如图(2),AE与BC交于点M,AC与EF交于点N,BC与EF交于点P.
(1)求证:AM=AN;
(2)当旋转角α=30°时,四边形ABPF是什么样的特殊四边形?并说明理由.
已知:正方形ABCD的边长为a,P是边CD上一个动点不与C、D重合,CP=b,以CP为一边在正方形ABCD外作正方形PCEF,连接BF、DF.
观察计算:
(1)如图1,当a=4,b=1时,四边形ABFD的面积为 _________
(2)如图2,当a=4,b=2时,四边形ABFD的面积为 _________ ;
(3)如图3,当a=4,b=3时,四边形ABFD的面积为 _________ ;
探索发现:
(4)根据上述计算的结果,你认为四边形ABFD的面积与正方形ABCD的面积之间有怎样的关系?证明你的结论;
(5)综合应用:农民赵大伯有一块正方形的土地(如图5),由于修路被占去一块三角形的地方△BCE,但决定在DE的右侧补给赵大伯一块土地,补偿后的土地为四边形ABMD,且四边形ABMD的面积与原来正方形土地的面积相等,M、E、B三点要在一条直线上,请你画图说明,如何确定M点的位置.
如图,正方形ABCD的边长为4,点E在对角线BD上,且∠BAE=22.5°,EF⊥AB,垂足为F,则EF的长为( )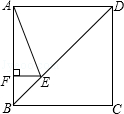
| A.1 | B.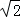 |
C.4﹣2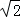 |
D.3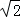 ﹣4 ﹣4 |
张大爷家有一块梯形形状的稻田(如图),已知:上底AD=400米,下底BC=600米,高h=300米,张大爷准备把这块稻田平均分给两个儿子(面积相等).
(1)分割方法有无数种,请你帮助张大爷设计两种不同的分割方案,在图1、图2中分别画出来,并简单说明理由;
(2)如果用竹篱笆将分给两个儿子的稻田隔开,问:分割线在什么位置时,所用篱笆长度最短?请在图3中画出来,并求出此时篱笆的最短长度.