如图,矩形纸片ABDC中,AB=5,AC=3,将纸片折叠,使点B落在边CD上的B′处,折痕为AE.在折痕A E上存在一点P到边CD的距离与到点B的距离相等,则此相等距离为__________.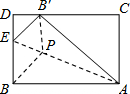
已知梯形ABCD中,AD∥BC,AB=15,CD=13,AD=8,∠B是锐角,∠B的正弦值为 ,那么BC的长为 .
,那么BC的长为 .
已知:如图,D是△ABC的边AB上一点,CN∥AB,DN交AC于点M,MA=MC.
①求证:AD=CN;
②若∠BAN=90度,求证:四边形ADCN是矩形.
如图,五边形ABCDE中,AB⊥BC,AE∥CD,∠A=∠E=120°,AB=CD=1,AE=2,则五边形ABCDE的面积等于 _________ .
如图,边长为1的菱形ABCD绕点A旋转,当B、C两点恰好落在扇形AEF的 上时,
上时, 的长度等于( ).
的长度等于( ).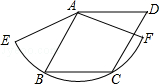
A.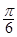 B.
B.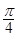 C.
C.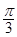 D.
D.
如图,点 是菱形
是菱形 的对角线
的对角线 上一点,连接
上一点,连接 并延长,交
并延长,交 于
于 ,交
,交 的延长线于点
的延长线于点 .
.
(1)图中△ 与哪个三角形全等?并说明理由.
与哪个三角形全等?并说明理由.
(2)求证:△ ∽△
∽△ .
.
(3)猜想:线段 ,
, ,
, 之间存在什么关系?并说明理由.
之间存在什么关系?并说明理由.
已知:如图所示的一张矩形纸片 ,将纸片折叠一次,使点
,将纸片折叠一次,使点 与
与 重合,再展开,折痕
重合,再展开,折痕 交
交 边于
边于 ,交
,交 边于
边于 ,分别连接
,分别连接 和
和 .
.
(1)求证:四边形 是菱形.
是菱形.
(2)若 ,△
,△ 的面积为
的面积为 ,求△
,求△ 的周长.
的周长.
(3)在线段 上是否存在一点
上是否存在一点 ,使得
,使得 ?若存在,请说明点
?若存在,请说明点 的位置,并予以证明;若不存在,请说明理由.
的位置,并予以证明;若不存在,请说明理由.
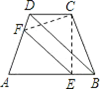
如图,四边形 为一梯形纸片,
为一梯形纸片,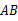 ∥
∥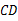 ,
,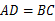 .翻折纸片
.翻折纸片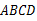 ,使点
,使点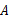 与点
与点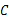 重合,折痕为
重合,折痕为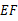 .已知
.已知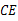 ⊥
⊥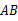 ,试说明:
,试说明: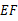 ∥
∥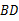 .
.
四边形是大家最熟悉的图形之一,我们已经发现了它的许多性质.只要善于观察、乐于探索,我们还会发现更多的结论.
(1)四边形一条对角线上任意一点与另外两个顶点的连线,将四边形分成四个三角形(如图①),其中相对的两对三角形的面积之积相等.你能证明这个结论吗?试试看.
已知:在四边形ABCD中,O是对角线BD上任意一点(如图①);
求证: .
.
证明:
(2)在三角形中(如图②),你能否归纳出类似的结论?若能,写出你猜想的结论,并证明;若不能,请说明理由.
如图,已知线段AB=10,AC=BD=2,点P是CD上一动点,分别以AP、PB为边向上、向下作正方形APEF和PHKB,设正方形对角线的交点分别为O1、O2,当点P从点C运动到点D时,线段O1O2中点G的运动路径的长是_____.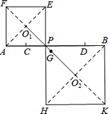
如图,在矩形ABCD中,点O是边AD上的中点,点E是边BC上的一个动点,延长EO到F,使得OE=OF.
(1)当点E运动到什么位置时,四边形AEDF是菱形?(直接写出答案)
(2)若矩形ABCD的周长为20,四边形AEDF的面积是否存在最大值?如果存在,请求出最大值;如果不存在,请说明理由.
(3)若AB= ,BC=
,BC= ,当
,当 .
. 满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
满足什么条件时,四边形AEDF能成为一个矩形?(不必说明理由)
如图,梯形ABCD中,AD//BC,AD=2,BC=8,AC=6,BD=8,则梯形ABCD的面积是 .
如图,矩形ABCD的对角线相交于点O,DE∥CA,AE∥BD.
(1)求证:四边形AODE是菱形;
(2)若将题设中“矩形ABCD”这一条件改为“菱形ABCD”,其余条件不变,则四边形AODE的形状是什么?说明理由.