初中数学圆试题

如图在边长为2的正方形ABCD中，E，F，O分别是AB，CD，AD的中点，以O为圆心，以OE为半径画弧EF.P是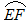上的一个动点，连结OP，并延长OP交线段BC于点K，过点P作⊙O的切线，分别交射线AB于点M，交直线BC于点G.

若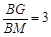，则BK﹦   ▲     .

如图，在等腰梯形ABCD中，AB∥CD， 对角线AC⊥BC，∠B＝60º，BC＝2cm，

则梯形ABCD的面积为（  ▲ ）

A．cm2

B．6 cm2

C．cm2

D．12 cm2

已知：如图，E，F分别是ABCD的边AD，BC的中点．求证：AF=CE．

如图，四边形ABCD中，∠BAD=∠ACB=90°，AB=AD，AC=4BC，
设CD的长为x，四边形ABCD的面积为y，则y与x之间的函数关系式是（　　）

A．

B．

C．

D．

如图，边长为(m+3)的正方形纸片剪出一个边长为m的正方形之后，剩余部分又剪拼成一个矩形(不重叠无缝隙)，若拼成的矩形一边长为3，则另一边长是（　　）

A．2m+3

B．2m+6

C．m+3

D．m+6

如图，在□ABCD中，点E、F是对角线AC上两点，且AE=CF．

求证：∠EBF=∠FDE．

如图，正方形纸片ABCD的边长为8，将其沿EF折叠，

则图中①②③④四个三角形的周长之和为 ▲  ．

如图，在平行四边形ABCD中，CD=10，F是AB边上一点，DF交AC于点E，

且=       ，BF=      .

（本小题满分8分）
　已知：如图，在正方形ABCD中，点E、F分别在BC和CD上，AE = AF．

（1）求证：BE = DF；
（2）连接AC交EF于点O，延长OC至点M，使OM = OA，连接EM、FM．判断四边形AEMF是什么特殊四边形？并证明你的结论．

．把一张矩形纸片（矩形ABCD）按如图方式折叠，使顶点B和点D重合，折痕为EF．若AB= 3 cm，BC= 5 cm，则重叠部分△DEF的面积是       cm²．

如图3，

在5×5正方形网格中，一条圆弧经过A，B，C三点，那么这条圆弧所在圆的圆心是

A．点P

B．点Q

C．点R

D．点M

如图2，在□ABCD中，AC平分∠DAB，AB = 3， 则□ABCD的周长为

A．6

B．9

C．12

D．15

如图，在梯形ABCD中，AB∥CD
（1）用尺规作图方法，作∠DAB的角平分线AF（只保留作图痕迹，不写作法和证明）
（2）若AF交CD边于点E，判断△ADE的形状（只写结果）

如图，P是菱形ABCD对角线BD上一点，PE⊥AB于点E，PE＝4cm，

则点P到BC的距离是_____cm.

如图，在梯形ABCD中，AD∥BC，∠B＝90°，BC＝6，AD＝3，∠DCB＝30°.点E、F同时从B点出发，沿射线BC向右匀速移动.已知F点移动速度是E点移动速度的2倍，以EF为一边在CB的上方作等边△EFG．设E点移动距离为x（x＞0）.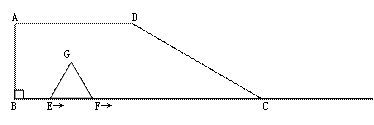

⑴△EFG的边长是____（用含有x的代数式表示），当x＝2时，点G的位置在_______；
⑵若△EFG与梯形ABCD重叠部分面积是y，求
①当0＜x≤2时，y与x之间的函数关系式；
②当2＜x≤6时，y与x之间的函数关系式；
⑶探求⑵中得到的函数y在x取含何值时，存在最大值，并求出最大值.