初中数学圆试题

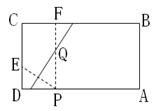
如图，四边形ABCD是正方形，BE⊥BF，BE=BF，EF与BC交于点G。

（1）求证：△ABE≌△CBF；
（2）若∠ABE=50º，求∠EGC的大小

如图，以正方形ABCD的对角线AC为一边，延长AB到E，使AE = AC，以AE为一边作菱形AEFC，若菱形的面积为，则正方形边长           

如图①，四边形ABCD是正方形,G是BC上任意一点，DE⊥AG于点E，BF⊥AG于点F.

⑴求证：DE－BF=EF．
⑵当点G为BC边中点时,试探究线段EF与GF之间的数量关系，并说明理由．
⑶若点G为CB延长线上一点，其余条件不变．请你在图②中画出图形，写出此时DE、BF、EF之间的数量关系，并说明理由．

如图，四边形ABCD中，E、F、G、H分别是AB、BC、CD、DA的中点.

⑴请判断四边形EFGH的形状？并说明为什么.
⑵若使四边形EFGH为正方形，那么四边形ABCD的对角线应具有怎样的性质？

如图,正方形ABCD的边长为2，将长为2的线段QR的两端放在正方形的相邻的两边上同时滑动．如果Q点从A点出发，沿图中所示方向按A→B→C→D→A滑动到A止，同时点R从B点出发，沿图中所示方向按B→C→D→A→B滑动到B止，在这个过程中，线段QR的中点M所经过的路线围成的图形的面积为

A．2

B．

C．

D．

不能判断四边形ABCD是平行四边形的是（　　）

A．AB＝CD，AD＝BC	B．AB＝CD，AB∥CD
C．AB＝CD，AD∥BC	D．AB∥CD，AD∥BC

如图1所示，长方形内有两个相邻的正方形，面积分别为4和2，那么阴影部分的面积为（　　　）

A．

B．

C．2

D．

已知Rt△ABC和Rt△EBC，°。以边AC上的点O为圆心、OA为半径的⊙O与EC相切，D为切点，AD//BC。
（1）用尺规确定并标出圆心O；（不写做法和证明，保留作图痕迹）
（2）求证：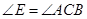
（3）若AD=1，，求BC的长。

如图，菱形ABCD中，AB=15,°，则B、D两点之间的距离为（ ）

A.15      B.       C.7.5          D.15

如图，是对角线上的两点，且.

求证：（1）；
（2）.

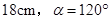如图，活动衣帽架由三个菱形组成，利用四边形的不稳定性，调整菱形的内角，使衣帽架拉伸或收缩.当菱形的边长为时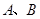，两点的距离为_______cm.

如图，有一块等腰梯形的草坪，草坪上底长48米，下底长108米，上下底相距40米，现要在草坪中修建一条横、纵向的“”型甬道，甬道宽度相等，甬道面积是整个梯形面积的.设甬道的宽为米.

（1）求梯形的周长；
（2）用含的式子表示甬道的总长；
（3）求甬道的宽是多少米？

(8分)如图7，已知，在ABCD中，AE=CF，M、N分别是DE、BF的中点.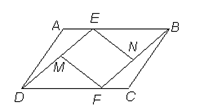

求证：四边形MFNE是平行四边形 .

如图，在ABCD中，已知AB=9㎝，AD=6㎝，BE平分∠ABC交DC边于点E，则DE等于         ㎝.

如图矩形纸片ABCD，AB＝5cm，BC＝10cm，CD上有一点E，ED＝2cm，AD上有一点P，PD＝3cm，过P作PF⊥AD交BC于F，将纸片折叠，使P点与E点重合，折痕与PF交于Q点，则PQ的长是____________cm