初中数学圆试题

已知平行四边形的一边长为，则对角线的长度可能取下列数组中的（  ）

A．、

B．、

C．、

D．、

顺次连结等腰梯形各边中点，所得的四边形一定是（  ）

A．等腰梯形

B．菱形

C．矩形

D．平行四边形

用两块完全相同的直角三角形拼下列图形：①平行四边形（不包含菱形、矩形、正方形）；②矩形；③菱形；④正方形；⑤等腰三角形；⑥等边三角形.一定能拼成的图形是（  ）

A．①④⑤

B．①②⑤

C．①②③

D．②⑤⑥

如图，△中，，、分別是△两个外角的平分线．
求证：；
若，试说明四边形是菱形．

.某铁路路基的横断面是一个等腰梯形（如图），若腰的坡比
为2：3，路基顶宽3米，高4米，则路基的下底宽为

A．7m

B．9m

C．12m

D．15m

下列说法正确的是（ ▲ ）                                            

A．对角线垂直的四边形是菱形

B．对角线垂直且相等的四边形是正方形

C．对角线相等的四边形是矩形

D．对角线相等的平行四边形是矩形

.如图，四边形为矩形纸片．把纸片折叠，使点恰好落在边的中点处，折痕为．若，则等
于（　 　）

A．

B．

C．

D．

 

某体育馆用大小相同的长方形木块镶嵌地面，第一次铺2块，如图（1）；第二次把第一次铺的完全围起来，如图（2），第三次把第二次铺的完全围起来，如图（3）；……以此方法，第n次铺完后，用字母n表示第几次镶嵌所使用的木块数为           。

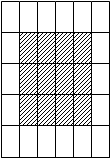
如图中的正方形的边长都相等，其中阴影部分面积相等的图形的个数是（   ）

A．1个

B．2个

C．3个

D．4个

如图，已知正方形A、矩形B、圆C的周长都是cm，其中矩形的长是宽的2倍，那么它们的面积、、之间的关系式正确的是（　　）.

A．＜＜
B．＜＜ 
C．＞＞
D．＞＞

如图，若将左图正方形剪成四块，恰能拼成右图的矩形，设，则 （ ）

A．

B．

C．

D．

）如图，等腰梯形ABCD中，AB=4，CD=9，∠C=60°，动点P从点C出发沿CD方向向点D运动，动点Q同时以相同速度从点D出发沿DA方向向终点A运动，其中一个动点到达端点时，另一个动点也随之停止运动.

求AD的长；
设CP=x， △PDQ的面积为y,求y关于x的函数表达式， 并求自变量的取值范围
探究：在BC边上是否存在点M使得四边形PDQM是菱形？若存在，请找出点M，并求出BM的长；不存在，请说明理由.

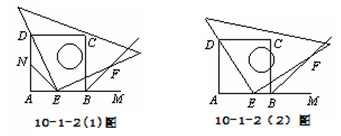
如图10－1－2（1），10－1－2（2），四边形ABCD是正方形，M是AB延长线上一点。直角三角尺的一条直角边经过点D，且直角顶点E在AB边上滑动（点E不与点A，B重合），另一条直角边与∠CBM的平分线BF相交于点F。
如图10－1－2（1），当点E在AB边的中点位置时：
①通过测量DE，EF的长度，猜想DE与EF满足的数量关系是         ；
②连接点E与AD边的中点N，猜想NE与BF满足的数量关系是             ；
③请证明你的上述两猜想。
如图10－1－2（2），当点E在AB边上的任意位置时，请你在AD边上找到一点N，使得NE=BF，进而猜想此时DE与EF有怎样的数量关系。

将一张等边三角形纸片沿着一边上的高剪开，可以拼成不同形状的四边形．试写出其中一种四边形的名称______________

顺次连结任意四边形各边中点所得到的四边形一定是                  

A．平行四边形

B．菱形

C．矩形

D．正方形