如果顺次连接四边形的各边中点得到的四边形是矩形,那么原来四边形的对角线一定满足的条件是
A.互相平分B.相等C.互相垂直D.互相垂直平分
下列说法:
①四边相等的四边形一定是菱形
②顺次连接矩形各边中点形成的四边形一定是正方形
③对角线相等的四边形一定是矩形
④经过平行四边形对角线交点的直线,一定能把平行四边形分成面积相等的两部分
其中正确的有 个.
A.4B.3C.2D.1
我们把顺次连接任意一个四边形各边中点所得的四边形叫做中点四边形.已知四边形 的中点四边形是正方形,对角线 与 的关系,下列说法正确的是
A. , 相等且互相平分B. , 垂直且互相平分
C. , 相等且互相垂直D. , 垂直且平分对角
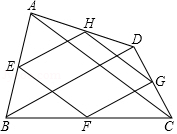
如图,点 、 、 、 分别是四边形 边 、 、 、 的中点.则下列说法:
①若 ,则四边形 为矩形;
②若 ,则四边形 为菱形;
③若四边形 是平行四边形,则 与 互相平分;
④若四边形 是正方形,则 与 互相垂直且相等.
其中正确的个数是
A.1B.2C.3D.4
如图, , 是四边形 的对角线,点 , 分别是 , 的中点,点 , 分别是 , 的中点,连接 , , , ,要使四边形 为正方形,则需添加的条件是
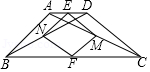
A. , B. , C. , D. ,
如图,已知点 、 、 、 分别是菱形 各边的中点,则四边形 是
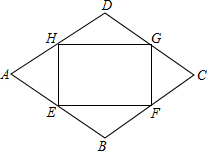
A.正方形B.矩形C.菱形D.平行四边形
如图,点 、 、 、 分别为四边形 的四边 、 、 、 的中点,则关于四边形 ,下列说法正确的为

A.一定不是平行四边形B.一定不是中心对称图形
C.可能是轴对称图形D.当 时它是矩形
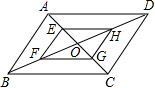
如图,▱ ABCD中, AB=2, AD=4,对角线 AC, BD相交于点 O,且 E, F, G, H分别是 AO, BO, CO, DO的中点,则下列说法正确的是( )
| A. |
EH=HG |
| B. |
四边形EFGH是平行四边形 |
| C. |
AC⊥BD |
| D. |
△ABO的面积是△EFO的面积的2倍 |
顺次连接菱形四边中点得到的四边形是
| A. |
平行四边形 |
B. |
菱形 |
C. |
矩形 |
D. |
正方形 |
如图,在菱形 中.点 、 、 、 分别是边 、 、 和 的中点,连接 、 、 和 .若 ,则下列结论正确的是

| A. |
|
B. |
|
C. |
|
D. |
|