初中数学矩形的性质选择题

在矩形 $\mathit{ABCD}$ 中， $\mathit{AC}$ 、 $\mathit{BD}$ 相交于点 $O$ ，若 $\mathit{\Delta AOB}$ 的面积为2，则矩形 $\mathit{ABCD}$ 的面积为 $($ 　　 $)$

A．

4

B．

6

C．

8

D．

10

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=2$ ， $\mathit{BC}=2\sqrt{5}$ ， $E$ 是 $\mathit{BC}$ 的中点，将 $\mathit{\Delta ABE}$ 沿直线 $\mathit{AE}$ 翻折，点 $B$ 落在点 $F$ 处，连结 $\mathit{CF}$ ，则 $\cos \angle \mathit{ECF}$ 的值为 $($ 　　 $)$

A．

$\frac{2}{3}$

B．

$\frac{\sqrt{10}}{4}$

C．

$\frac{\sqrt{5}}{3}$

D．

$\frac{2\sqrt{5}}{5}$

将一张矩形纸片折叠成如图所示的图形，若 $\angle \mathit{CAB}=30°$ ，则 $\angle \mathit{ACB}$ 的度数是 $($ 　　 $)$

A．

$45°$

B．

$55°$

C．

$65°$

D．

$75°$

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=3$ ， $\mathit{BC}=4$ ，动点 $P$ 沿折线 $\mathit{BCD}$ 从点 $B$ 开始运动到点 $D$ ，设点 $P$ 运动的路程为 $x$ ， $\mathit{\Delta ADP}$ 的面积为 $y$ ，那么 $y$ 与 $x$ 之间的函数关系的图象大致是 $($ 　　 $)$

A．		B．
C．		D．

如图，将矩形 $\mathit{ABCD}$ 沿 $\mathit{AC}$ 折叠，使点 $B$ 落在点 $B\text{'}$ 处， $B\text{'}C$ 交 $\mathit{AD}$ 于点 $E$ ，若 $\angle 1=25°$ ，则 $\angle 2$ 等于 $($ 　　 $)$

A．

$25°$

B．

$30°$

C．

$50°$

D．

$60°$

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=3$ ， $\mathit{BC}=10$ ，点 $E$ 在 $\mathit{BC}$ 边上， $\mathit{DF}\perp \mathit{AE}$ ，垂足为 $F$ ．若 $\mathit{DF}=6$ ，则线段 $\mathit{EF}$ 的长为 $($ 　　 $)$

A．

2

B．

3

C．

4

D．

5

如图，矩形 $\mathit{ABCD}$ 的对角线 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $O$ ， $\mathit{AB}=6$ ， $\mathit{BC}=8$ ，过点 $O$ 作 $\mathit{OE}\perp \mathit{AC}$ ，交 $\mathit{AD}$ 于点 $E$ ，过点 $E$ 作 $\mathit{EF}\perp \mathit{BD}$ ，垂足为 $F$ ，则 $\mathit{OE}+\mathit{EF}$ 的值为 $($ 　　 $)$

A．

$\frac{48}{5}$

B．

$\frac{32}{5}$

C．

$\frac{24}{5}$

D．

$\frac{12}{5}$

矩形具有而平行四边形不一定具有的性质是 $($ 　　 $)$

A．	对边相等	B．	对角相等
C．	对角线相等	D．	对角线互相平分

如图，矩形 $\mathit{ABCD}$ 的顶点 $A$ ， $B$ ， $C$ 分别落在 $\angle \mathit{MON}$ 的边 $\mathit{OM}$ ， $\mathit{ON}$ 上，若 $\mathit{OA}=\mathit{OC}$ ，要求只用无刻度的直尺作 $\angle \mathit{MON}$ 的平分线．小明的作法如下：连接 $\mathit{AC}$ ， $\mathit{BD}$ 交于点 $E$ ，作射线 $\mathit{OE}$ ，则射线 $\mathit{OE}$ 平分 $\angle \mathit{MON}$ ．有以下几条几何性质：①矩形的四个角都是直角，②矩形的对角线互相平分，③等腰三角形的"三线合一"．小明的作法依据是 $($ 　　 $)$

A．

①②

B．

①③

C．

②③

D．

①②③

如图，矩形 $\mathit{ABCD}$ 中， $\mathit{AC}$ 与 $\mathit{BD}$ 相交于点 $E$ ， $\mathit{AD}:\mathit{AB}=\sqrt{3}:1$ ，将 $\mathit{\Delta ABD}$ 沿 $\mathit{BD}$ 折叠，点 $A$ 的对应点为 $F$ ，连接 $\mathit{AF}$ 交 $\mathit{BC}$ 于点 $G$ ，且 $\mathit{BG}=2$ ，在 $\mathit{AD}$ 边上有一点 $H$ ，使得 $\mathit{BH}+\mathit{EH}$ 的值最小，此时 $\frac{\mathit{BH}}{\mathit{CF}}=($ 　　 $)$

A．

$\frac{\sqrt{3}}{2}$

B．

$\frac{2\sqrt{3}}{3}$

C．

$\frac{\sqrt{6}}{2}$

D．

$\frac{3}{2}$

如图，对折矩形纸片 $\mathit{ABCD}$ ，使 $\mathit{AD}$ 与 $\mathit{BC}$ 重合，得到折痕 $\mathit{EF}$ ．把纸片展平，再一次折叠纸片，使点 $A$ 落在 $\mathit{EF}$ 上的点 $A\text{'}$ 处，并使折痕经过点 $B$ ，得到折痕 $\mathit{BM}$ ．若矩形纸片的宽 $\mathit{AB}=4$ ，则折痕 $\mathit{BM}$ 的长为 $($ 　　 $)$

A．

$\frac{8\sqrt{3}}{3}$

B．

$\frac{4\sqrt{3}}{3}$

C．

8

D．

$8\sqrt{3}$

对于任意的矩形，下列说法一定正确的是 $($ 　　 $)$

A．	对角线垂直且相等
B．	四边都互相垂直
C．	四个角都相等
D．	是轴对称图形，但不是中心对称图形

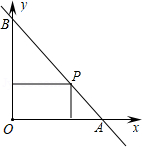
如图，一直线与两坐标轴的正半轴分别交于 $A$ ， $B$ 两点， $P$ 是线段 $\mathit{AB}$ 上任意一点（不包括端点），过点 $P$ 分别作两坐标轴的垂线与两坐标轴围成的矩形的周长为8，则该直线的函数表达式是 $($ 　　 $)$

A．

$y=-x+4$

B．

$y=x+4$

C．

$y=x+8$

D．

$y=-x+8$

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=2$ ， $\mathit{BC}=3$ ，动点 $P$ 沿折线 $\mathit{BCD}$ 从点 $B$ 开始运动到点 $D$ ．设运动的路程为 $x$ ， $\mathit{\Delta ADP}$ 的面积为 $y$ ，那么 $y$ 与 $x$ 之间的函数关系的图象大致是 $($ 　　 $)$

A．		B．
C．		D．

如图，矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=4$ ， $\mathit{AD}=2$ ， $E$ 为 $\mathit{AB}$ 的中点， $F$ 为 $\mathit{EC}$ 上一动点， $P$ 为 $\mathit{DF}$ 中点，连接 $\mathit{PB}$ ，则 $\mathit{PB}$ 的最小值是 $($ 　　 $)$

A．

2

B．

4

C．

$\sqrt{2}$

D．

$2\sqrt{2}$