如图,在 中, , , 为 边的中点,线段 的垂直平分线交边 于点 .设 , ,则

A. B. C. D.
如图,点 , 在反比例函数 的图象上, 轴, 轴,垂足 , 分别在 轴的正、负半轴上, ,已知 , 是 的中点,且 的面积是 的面积的2倍,则 的值是 .
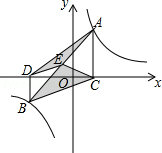
如图1,在直角坐标系 中,直线 交 轴, 轴于点 , ,点 的坐标是 ,过点 分别作 轴、 轴的垂线,垂足为 、 ,点 是线段 上的动点,以 为对称轴,作与 成轴对称的△ .
(1)当 时,求点 的坐标.
(2)当图1中的直线 经过点 ,且 时(如图 ,求点 由 到 的运动过程中,线段 扫过的图形与 重叠部分的面积.
(3)当图1中的直线 经过点 , 时(如图 ,以 为对称轴,作与 成轴对称的△ ,连接 , ,问是否存在点 ,使得△ 与△ 相似?若存在,求出 、 的值;若不存在,请说明理由.
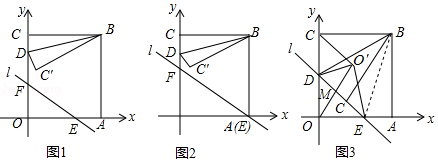
如图1,我们把对角线互相垂直的四边形叫做垂美四边形.
(1)概念理解:如图2,在四边形 中, , ,问四边形 是垂美四边形吗?请说明理由.
(2)性质探究:试探索垂美四边形 两组对边 , 与 , 之间的数量关系.
猜想结论:(要求用文字语言叙述)
写出证明过程(先画出图形,写出已知、求证).
(3)问题解决:如图3,分别以 的直角边 和斜边 为边向外作正方形 和正方形 ,连接 , , ,已知 , ,求 长.

如图, 为 的直径,弦 ,垂足为点 ,直线 与 的延长线交于点 ,且 .
(1)求证:直线 是 的切线.
(2)若 , ,求线段 的长.

如图,在菱形 中,过点 作 , ,垂足分别为点 , ,延长 至 ,使得 ,连接 , ,若 ,则 .

由6根钢管首尾顺次铰接而成六边形钢架 ,相邻两钢管可以转动.已知各钢管的长度为 米, 米.(铰接点长度忽略不计)
(1)转动钢管得到三角形钢架,如图1,则点 , 之间的距离是 米.
(2)转动钢管得到如图2所示的六边形钢架,有 ,现用三根钢条连接顶点使该钢架不能活动,则所用三根钢条总长度的最小值是 米.

如图, 纸片中, , , ,点 在边 上,以 为折痕 折叠得到△ , 与边 交于点 .若 为直角三角形,则 的长是 .

如图,在 中, , , ,分别以点 , 为圆心,大于线段 长度一半的长为半径作弧,相交于点 , ,过点 , 作直线 ,交 于点 ,连接 ,则 的长是 .
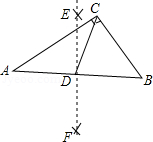
在线段 的同侧作射线 和 ,若 与 的平分线分别交射线 , 于点 , , 和 交于点 .如图,点点同学发现当射线 , 交于点 ;且 时,有以下两个结论:
① ;② .
那么,当 时:
(1)点点发现的结论还成立吗?若成立,请给予证明;若不成立,请求出 的度数,写出 , , 长度之间的等量关系,并给予证明;
(2)设点 为线段 上一点, ,若 ,四边形 的面积为 ,求 的长.

如图,已知四边形 和四边形 为正方形,点 在线段 上,点 , , 在同一直线上,且 , ,连接 , , ,并延长 交 于点 .
(1)求 的值.
(2)求线段 的长.

已知直角三角形纸片的两条直角边长分别为 和 ,过锐角顶点把该纸片剪成两个三角形,若这两个三角形都为等腰三角形,则
A. B. C. D.
如图,将矩形 的四个角向内翻折后,恰好拼成一个无缝隙无重叠的四边形 , 厘米, 厘米,则边 的长是

A.12厘米B.16厘米C.20厘米D.28厘米