初中数学勾股定理填空题

如图是我国汉代数学家赵爽在注解《周髀算经》时给出的“赵爽弦图”，图中的四个直角三角形是全等的，如果大正方形ABCD的面积是小正方形EFGH面积的13倍，那么 $\mathit{tan}\angle \mathit{ADE}$的值为　　．

在Rt△ ABC中，∠ C＝90°， AD平分∠ CAB， BE平分∠ ABC， AD、 BE相交于点 F，且 AF＝4， EF＝ $\sqrt{2}$ ，则 AC＝ 　．

腰长为5，高为4的等腰三角形的底边长为 　　．

如图，在矩形 ABCD中， AD＝8，对角线 AC与 BD相交于点 O， AE⊥ BD，垂足为点 E，且 AE平分∠ BAC，则 AB的长为 　　．

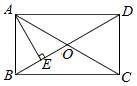
如图1， AF， BE是△ ABC的中线， AF⊥ BE，垂足为点 P，设 BC＝ a， AC＝ b， AB＝ c，则 a ²+ b ²＝5 c ²，利用这一性质计算．如图2，在▱ ABCD中， E， F， G分别是 AD， BC， CD的中点， EB⊥ EG于点 E， AD＝8， AB＝2 $\sqrt{5}$ ，则 AF＝ 　　．

如图，在四边形ABCD中， $\angle \mathit{ABC}＝90°$， $\mathit{AB}＝3$， $\mathit{BC}＝4$， $\mathit{CD}＝10$， $\mathit{DA}=5\sqrt{5}$，则BD的长为　   　．

如图，在▱ABCD中， $\mathit{AB}=2\sqrt{13}\text{cm}$， $\mathit{AD}＝4\mathit{cm}，$ $\mathit{AC}\perp \mathit{BC}$，则△DBC比△ABC的周长长　　cm．

如图，AB＝6，O是AB的中点，直线l经过点O，∠1＝120°，P是直线l上一点，当△APB为直角三角形时，AP＝　    　．

如图，在正方形 ABCD中，点 E， F分别在 BC， CD上，如果 AE＝3， EF＝2， AF＝ $\sqrt{\text{13}}$ ，那么正方形 ABCD的边长等于 　．

如图，矩形纸片 中， ， ，先按图（2）操作：将矩形纸片 沿过点 的直线折叠，使点 落在边 上的点 处，折痕为 ；再按图（3）操作，沿过点 的直线折叠，使点 落在 上的点 处，折痕为 ，则 、 两点间的距离为 　　．

如图，在 中， ， ， ， ， ，点 在 上， 交 于点 ， 交 于点 ，当 时， 　　．

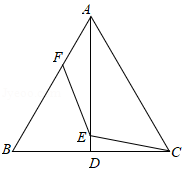
如图， $\mathit{\Delta ABC}$ 为等边三角形，边长为6， $\mathit{AD}\perp \mathit{BC}$ ，垂足为点 $D$ ，点 $E$ 和点 $F$ 分别是线段 $\mathit{AD}$ 和 $\mathit{AB}$ 上的两个动点，连接 $\mathit{CE}$ ， $\mathit{EF}$ ，则 $\mathit{CE}+\mathit{EF}$ 的最小值为 　 　．

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=6$ ， $\mathit{BC}=8$ ，对角线 $\mathit{AC}$ ， $\mathit{BD}$ 相交于点 $O$ ，点 $P$ 为边 $\mathit{AD}$ 上一动点，连接 $\mathit{OP}$ ，以 $\mathit{OP}$ 为折痕，将 $\mathit{\Delta AOP}$ 折叠，点 $A$ 的对应点为点 $E$ ，线段 $\mathit{PE}$ 与 $\mathit{OD}$ 相交于点 $F$ ．若 $\mathit{\Delta PDF}$ 为直角三角形，则 $\mathit{DP}$ 的长为 　 　．

如图，在矩形 $\mathit{ABCD}$ 中， $\mathit{AB}=1$ ， $\mathit{BC}=2$ ，点 $E$ 和点 $F$ 分别为 $\mathit{AD}$ ， $\mathit{CD}$ 上的点，将 $\mathit{\Delta DEF}$ 沿 $\mathit{EF}$ 翻折，使点 $D$ 落在 $\mathit{BC}$ 上的点 $M$ 处，过点 $E$ 作 $\mathit{EH}//\mathit{AB}$ 交 $\mathit{BC}$ 于点 $H$ ，过点 $F$ 作 $\mathit{FG}//\mathit{BC}$ 交 $\mathit{AB}$ 于点 $G$ ．若四边形 $\mathit{ABHE}$ 与四边形 $\mathit{BCFG}$ 的面积相等，则 $\mathit{CF}$ 的长为 　　．

如图，菱形 $\mathit{ABCD}$ 的边长为4， $\angle A=45°$ ，分别以点 $A$ 和点 $B$ 为圆心，大于 $\frac{1}{2}\mathit{AB}$ 的长为半径作弧，两弧相交于 $M$ ， $N$ 两点，直线 $\mathit{MN}$ 交 $\mathit{AD}$ 于点 $E$ ，连接 $\mathit{CE}$ ，则 $\mathit{CE}$ 的长为 　 　．