如图,点 是矩形纸片 的对称中心, 是 上一点,将纸片沿 折叠后,点 恰好与点 重合.若 ,则折痕 的长为 .

如图,已知点 在正方形 的边 上,以 为边向正方形 外部作正方形 ,连接 , 、 分别是 、 的中点,连接 .若 , ,则 .
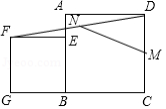
如图,有一张长方形纸片 , , ,点 为 上一点,将纸片沿 折叠, 的对应边 恰好经过点 ,则线段 的长为 .

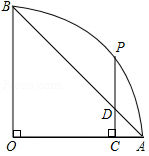
如图,扇形 中, . 为弧 上的一点,过点 作 ,垂足为 , 与 交于点 .若 , ,则该扇形的半径长为 .
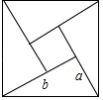
我国古代数学家赵爽的“勾股圆方图”是由四个全等的直角三角形与中间的一个小正方形拼成的一个大正方形(如图所示).如果大正方形的面积是13,小正方形的面积是1,直角三角形的两直角边长分别为 、 ,那么 的值是 .
中, , , ,过点 的直线把 分割成两个三角形,使其中只有一个是等腰三角形,则这个等腰三角形的面积是 .
如图,正方形 的边长为12,点 在边 上, ,过点 作 ,分别交 、 于 、 两点.若点 、 分别为 、 的中点,则 的长为 .
