已知抛物线 与 轴交于点 ,与直线 为任意实数)相交于 , 两点,则下列结论不正确的是
| A. |
存在实数 ,使得 为等腰三角形 |
| B. |
存在实数 ,使得 的内角中有两角分别为 和 |
| C. |
任意实数 ,使得 都为直角三角形 |
| D. |
存在实数 ,使得 为等边三角形 |
如图, 的顶点 是边长为2的等边 的重心, 的两边与 的边交于 , , ,则 与 的边所围成阴影部分的面积是
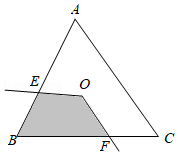
| A. |
|
B. |
|
C. |
|
D. |
|
如图,四边形 是边长为1的正方形, 是等边三角形,连接 并延长交 的延长线于点 ,连接 交 于点 ,下列结论:
① ;② ;③ ;④ .
其中正确的有

| A. |
①②③ |
B. |
②③④ |
C. |
①③④ |
D. |
①②④ |
已知 的对角线 、 相交于点 , 是等边三角形,且 ,则 等于
| A. |
2 |
B. |
4 |
C. |
|
D. |
|
如图,边长都为4的正方形 和正三角形 如图放置, 与 在一条直线上,点 与点 重合.现将 沿 方向以每秒1个单位的速度匀速运动,当点 与 重合时停止.在这个运动过程中,正方形 和 重叠部分的面积 与运动时间 的函数图象大致是

| A. |
|
B. |
|
C. |
|
D. |
|
如图,在直角坐标系中,已知点,等边三角形
的顶点
在反比例函数
的图象上.
(1)求反比例函数的表达式.
(2)把向右平移
个单位长度,对应得到△
当这个函数图象经过△
一边的中点时,求
的值.

如图,等边三角形 的边长为8,以 上一点 为圆心的圆分别与边 , 相切,则 的半径为

| A. |
|
B. |
3 |
C. |
4 |
D. |
|
如图,取两根等宽的纸条折叠穿插,拉紧,可得边长为2的正六边形.则原来的纸带宽为

| A. |
1 |
B. |
|
C. |
|
D. |
2 |
如图1,经过等边
的顶点
,
(圆心
在
内),分别与
,
的延长线交于点
,
,连结
,
交
于点
.
(1)求证:.
(2)当,
时,求
的长.
(3)设,
.
①求关于
的函数表达式;
②如图2,连结,
,若
的面积是
面积的10倍,求
的值.

如图,已知是
的直径,
是
上的点,点
在
的延长线上,
.
(1)求证:是
的切线;
(2)若,
,求图中阴影部分的面积.

请阅读下列材料,并完成相应的任务:
阿基米德折弦定理
阿基米德 ,公元前 公元前212年,古希腊)是有史以来最伟大的数学家之一,他与牛顿、高斯并称为三大数学王子.
阿拉伯 年)的译文中保存了阿基米德折弦定理的内容,苏联在1964年根据 译本出版了俄文版《阿基米德全集》,第一题就是阿基米德折弦定理.
阿基米德折弦定理:如图1, 和 是 的两条弦(即折线 是圆的一条折弦), , 是 的中点,则从 向 所作垂线的垂足 是折弦 的中点,即 .下面是运用"截长法"证明 的部分证明过程.证明:如图2,在 上截取 ,连接 , , 和 .
是 的中点,
.
任务:
(1)请按照上面的证明思路,写出该证明的剩余部分;
(2)填空:如图3,已知等边 内接于 , , 为 上一点, , 于点 ,则 的周长是 .