初中数学等边三角形的性质试题

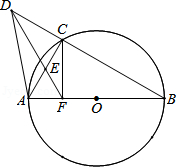
已知AB是半径为1的圆O直径，C是圆上一点，D是BC延长线上一点，过点D的直线交AC于E点，且△AEF为等边三角形

（1）求证：△DFB是等腰三角形；

（2）若 $\mathit{DA}＝\sqrt{7}\mathit{AF}$，求证： $\mathit{CF}\perp \mathit{AB}$．

问题探究：

1．新知学习

若把将一个平面图形分为面积相等的两个部分的直线叫做该平面图形的“面线”，其“面线”被该平面图形截得的线段叫做该平面图形的“面径”（例如圆的直径就是圆的“面径”）．

2．解决问题

已知等边三角形ABC的边长为2．

（1）如图一，若 $\mathit{AD}\perp \mathit{BC}$，垂足为D，试说明AD是△ABC的一条面径，并求AD的长；

（2）如图二，若 $\mathit{ME}\parallel \mathit{BC}$，且ME是△ABC的一条面径，求面径ME的长；

（3）如图三，已知D为BC的中点，连接AD，M为AB上的一点 $（0＜\mathit{AM}＜1）$，E是DC上的一点，连接ME，ME与AD交于点O，且 $S_{△\mathit{MOA}}＝S_{△\mathit{DOE}}$．

①求证：ME是△ABC的面径；

②连接AE，求证： $\mathit{MD}\parallel \mathit{AE}$；

（4）请你猜测等边三角形ABC的面径长l的取值范围（直接写出结果）

已知菱形 ABCD， E、 F是动点，边长为4， BE＝ AF，∠ BAD＝120°，则下列结论正确的有几个（　　）

①△ BEC≌△ AFC；②△ ECF为等边三角形；③∠ AGE＝∠ AFC；④若 AF＝1，则 $\frac{\mathit{GF}}{\mathit{EG}}$ ＝ $\frac{1}{3}$ ．

A．

1

B．

2

C．

3

D．

4

如图，等边△ ABC中， AB＝6，点 D在 BC上， BD＝4，点 E为边 AC上一动点（不与点 C重合），△ CDE关于 DE的轴对称图形为△ FDE．

（1）当点 F在 AC上时，求证： DF∥ AB；

（2）设△ ACD的面积为 S ₁，△ ABF的面积为 S ₂，记 S＝ S ₁﹣ S ₂， S是否存在最大值？若存在，求出 S的最大值；若不存在，请说明理由；

（3）当 B， F， E三点共线时．求 AE的长．

如图，已知等边△ OA ₁ B ₁，顶点 A ₁在双曲线 y＝ $\frac{\sqrt{3}}{x}$ （ x＞0）上，点 B ₁的坐标为（2，0）．过 B ₁作 B ₁ A ₂∥ OA ₁交双曲线于点 A ₂，过 A ₂作 A ₂ B ₂∥ A ₁ B ₁交 x轴于点 B ₂，得到第二个等边△ B ₁ A ₂ B ₂；过 B ₂作 B ₂ A ₃∥ B ₁ A ₂交双曲线于点 A ₃，过 A ₃作 A ₃ B ₃∥ A ₂ B ₂交 x轴于点 B ₃，得到第三个等边△ B ₂ A ₃ B ₃；以此类推，…，则点 B ₆的坐标为 　．

如图，在正方形 ABCD的外侧，作等边△ ABE，则∠ BED为（　　）

A．

15°

B．

35°

C．

45°

D．

55°

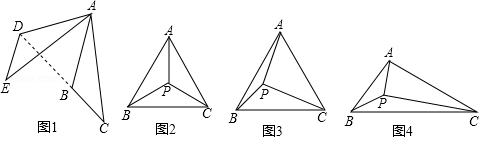
（1）【操作发现】

如图1，将△ ABC绕点 A顺时针旋转60°，得到△ ADE，连接 BD，则∠ ABD＝ 　　度．

（2）【类比探究】

如图2，在等边三角形 ABC内任取一点 P，连接 PA， PB， PC，求证：以 PA， PB， PC的长为三边必能组成三角形．

（3）【解决问题】

如图3，在边长为 $\sqrt{7}$ 的等边三角形 ABC内有一点 P，∠ APC＝90°，∠ BPC＝120°，求△ APC的面积．

（4）【拓展应用】

如图4是 A， B， C三个村子位置的平面图，经测量 AC＝4， BC＝5，∠ ACB＝30°， P为△ ABC内的一个动点，连接 PA， PB， PC．求 PA+ PB+ PC的最小值．

如图，将边长为10的正三角形OAB放置于平面直角坐标系xOy中，C是AB边上的动点（不与端点A，B重合），作CD⊥OB于点D，若点C，D都在双曲线 $y=\frac{\text{k}}{\text{x}}$上 $（k＞0，x＞0）$，则k的值为（　　）

A． $25\sqrt{3}$B． $18\sqrt{3}$C． $9\sqrt{3}$D．9

如图，以边长为20 cm的正三角形铁皮的各顶点为端点，在各边上分别截取6 cm长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则这个盒子的容积为 　　 cm ³．

如图，以边长为20cm的正三角形铁皮的各顶点为端点，在各边上分别截取6cm长的六条线段，过截得的六个端点作所在边的垂线，形成三个有两个直角的四边形．把它们沿虚线剪掉，用剩下的纸板折成一个底为正三角形的无盖柱形盒子，则这个盒子的容积为　　cm³．

如图，边长为2的等边△ABC和边长为1的等边△A′B′C′，它们的边B′C′，BC位于同一条直线l上，开始时，点C′与B重合，△ABC固定不动，然后把△A′B′C′自左向右沿直线l平移，移出△ABC外（点B′与C重合）停止，设△A′B′C′平移的距离为x，两个三角形重合部分的面积为y，则y关于x的函数图象是（　　）

A．B．

C．D．

如图，是等边三角形，平分，点在的延长线上，且，，则　　．

如图，∠MON＝60°，作边长为1的正六边形A₁B₁C₁D₁E₁F₁，边A₁B₁、F₁E₁分别在射线OM、ON上，边C₁D₁所在的直线分别交OM、ON于点A₂、F₂，以A₂F₂为边作正六边形A₂B₂C₂D₂E₂F₂，边C₂D₂所在的直线分别交OM、ON于点A₃、F₃，再以A₃F₃为边作正六边形A₃B₃C₃D₃E₃F₃，…，依此规律，经第n次作图后，点B_n到ON的距离是　　．

如图，在△ABC中，分别以AC、BC为边作等边三角形ACD和等边三角形BCE，连接AE、BD交于点O，则∠AOB的度数为　　．

已知 $\mathit{AB}$ 为 $\odot O$ 的直径且长为 $2r$ ， $C$ 为 $\odot O$ 上异于 $A$ ， $B$ 的点，若 $\mathit{AD}$ 与过点 $C$ 的 $\odot O$ 的切线互相垂直，垂足为 $D$ ．①若等腰三角形 $\mathit{AOC}$ 的顶角为120度，则 $\mathit{CD}=\frac{1}{2}r$ ，②若 $\mathit{\Delta AOC}$ 为正三角形，则 $\mathit{CD}=\frac{\sqrt{3}}{2}r$ ，③若等腰三角形 $\mathit{AOC}$ 的对称轴经过点 $D$ ，则 $\mathit{CD}=r$ ，④无论点 $C$ 在何处，将 $\mathit{\Delta ADC}$ 沿 $\mathit{AC}$ 折叠，点 $D$ 一定落在直径 $\mathit{AB}$ 上，其中正确结论的序号为 　．