如图,以边长为20cm的正三角形铁皮的各顶点为端点,在各边上分别截取6cm长的六条线段,过截得的六个端点作所在边的垂线,形成三个有两个直角的四边形.把它们沿虚线剪掉,用剩下的纸板折成一个底为正三角形的无盖柱形盒子,则这个盒子的容积为 cm3.

如图,边长为2的等边△ABC和边长为1的等边△A′B′C′,它们的边B′C′,BC位于同一条直线l上,开始时,点C′与B重合,△ABC固定不动,然后把△A′B′C′自左向右沿直线l平移,移出△ABC外(点B′与C重合)停止,设△A′B′C′平移的距离为x,两个三角形重合部分的面积为y,则y关于x的函数图象是( )

A. B.
B.
C. D.
D.
如图,∠MON=60°,作边长为1的正六边形A1B1C1D1E1F1,边A1B1、F1E1分别在射线OM、ON上,边C1D1所在的直线分别交OM、ON于点A2、F2,以A2F2为边作正六边形A2B2C2D2E2F2,边C2D2所在的直线分别交OM、ON于点A3、F3,再以A3F3为边作正六边形A3B3C3D3E3F3,…,依此规律,经第n次作图后,点Bn到ON的距离是 .

如图,在△ABC中,分别以AC、BC为边作等边三角形ACD和等边三角形BCE,连接AE、BD交于点O,则∠AOB的度数为 .

已知 为 的直径且长为 , 为 上异于 , 的点,若 与过点 的 的切线互相垂直,垂足为 .①若等腰三角形 的顶角为120度,则 ,②若 为正三角形,则 ,③若等腰三角形 的对称轴经过点 ,则 ,④无论点 在何处,将 沿 折叠,点 一定落在直径 上,其中正确结论的序号为 .
如图,在等边 中, ,点 , 分别在边 , 上,且 ,连接 , 交于点 ,连接 ,则 的最小值是 .

如图,以 为边,在 的同侧分别作正五边形 和等边 ,连接 , ,则 的度数是 .

如图, 为等边三角形,边长为6, ,垂足为点 ,点 和点 分别是线段 和 上的两个动点,连接 , ,则 的最小值为 .
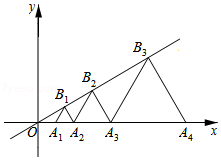
如图,在平面直角坐标系中,点 , , , , 在 轴正半轴上,点 , , , 在直线 上,若 ,且△ ,△ ,△ , 均为等边三角形,则线段 的长度为
| A. |
|
B. |
|
C. |
|
D. |
|
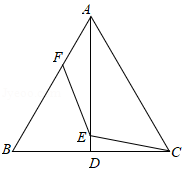
如图, 是等边三角形, ,动点 从点 出发,以 的速度沿 向点 匀速运动,过点 作 ,交折线 于点 ,以 为边作等边三角形 ,使点 , 在 异侧.设点 的运动时间为 , 与 重叠部分图形的面积为 .
(1) 的长为 (用含 的代数式表示).
(2)当点 落在边 上时,求 的值.
(3)求 关于 的函数解析式,并写出自变量 的取值范围.

如图,正方形 的边长为6, 为 的中点, 为等边三角形,过点 作 的垂线分别与边 、 相交于点 、 ,点 、 分别在线段 、 上运动,且满足 ,连接 .
(1)求证: .
(2)当点 在线段 上时,试判断 的值是否变化?如果不变,求出这个值,如果变化,请说明理由.
(3)设 ,点 关于 的对称点为 ,若点 落在 的内部,试写出 的范围,并说明理由.
