如图, 为等边三角形,点 从 出发,沿 作匀速运动,则线段 的长度 与运动时间 之间的函数关系大致是

A. B.
B.
C. D.
D.
已知等边 的边长为12, 是 上的动点,过 作 于点 ,过 作 于点 ,过 作 于点 .当 与 重合时, 的长是
A.3B.4C.8D.9
如图,边长为4的等边 中, 、 分别为 , 的中点,则 的面积是
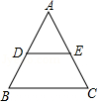
A. B. C. D.
已知等边三角形的边长为3,点 为等边三角形内任意一点,则点 到三边的距离之和为
A. B. C. D.不能确定
如图,点 是边长为 的等边 的内心,将 绕点 逆时针旋转 得到△ , 交 于点 , 交 于点 ,则 .

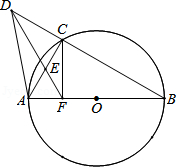
如图,点 是等边三角形 外接圆上一点. 是 上一点,且满足 ,点 是 与 的交点.
(1)求证: ;
(2)如果 , .求线段 的长及 的面积.

已知AB是半径为1的圆O直径,C是圆上一点,D是BC延长线上一点,过点D的直线交AC于E点,且△AEF为等边三角形
(1)求证:△DFB是等腰三角形;
(2)若 ,求证: .
已知菱形 ABCD, E、 F是动点,边长为4, BE= AF,∠ BAD=120°,则下列结论正确的有几个( )
①△ BEC≌△ AFC;②△ ECF为等边三角形;③∠ AGE=∠ AFC;④若 AF=1,则 = .

| A. |
1 |
B. |
2 |
C. |
3 |
D. |
4 |
如图,等边△ ABC中, AB=6,点 D在 BC上, BD=4,点 E为边 AC上一动点(不与点 C重合),△ CDE关于 DE的轴对称图形为△ FDE.
(1)当点 F在 AC上时,求证: DF∥ AB;
(2)设△ ACD的面积为 S 1,△ ABF的面积为 S 2,记 S= S 1﹣ S 2, S是否存在最大值?若存在,求出 S的最大值;若不存在,请说明理由;
(3)当 B, F, E三点共线时.求 AE的长.

如图,已知等边△ OA 1 B 1,顶点 A 1在双曲线 y= ( x>0)上,点 B 1的坐标为(2,0).过 B 1作 B 1 A 2∥ OA 1交双曲线于点 A 2,过 A 2作 A 2 B 2∥ A 1 B 1交 x轴于点 B 2,得到第二个等边△ B 1 A 2 B 2;过 B 2作 B 2 A 3∥ B 1 A 2交双曲线于点 A 3,过 A 3作 A 3 B 3∥ A 2 B 2交 x轴于点 B 3,得到第三个等边△ B 2 A 3 B 3;以此类推,…,则点 B 6的坐标为 .

如图,在正方形 ABCD的外侧,作等边△ ABE,则∠ BED为( )

| A. |
15° |
B. |
35° |
C. |
45° |
D. |
55° |
如图,将边长为10的正三角形OAB放置于平面直角坐标系xOy中,C是AB边上的动点(不与端点A,B重合),作CD⊥OB于点D,若点C,D都在双曲线 上 ,则k的值为( )

A. B. C. D.9